题目内容
已知两个方程x2+4x+4a=0①和x2+3x+6a=0②都有两个不同的实数根,并且一个方程的任意一个根不在另一个方程的两个根之间,试问满足上述的实数a是否存在?若存在,求出实数a;若不存在,请说明理由.
解析:方程①有两个不同的实根的充要条件是Δ=42-4×4a>0,即a<1.?
方程②有两个不同的实根的充要条件是Δ′=32-4×6a>0,即a<![]() .?
.?
于是,当a<![]() 时,两个方程都有不同的实根.?
时,两个方程都有不同的实根.?
在a<![]() 的条件下,方程①的两个根是
的条件下,方程①的两个根是
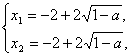
并且x1<x2,方程②的两个根是?
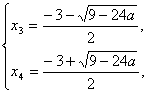
并且x3<x4.?
要使一个方程的任意一个根不在另一个方程两个根之间,a的值应满足下列两组条件之一.
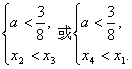
首先解x2<x3的情形,即?
-2+2![]() <
<![]()
-1+4![]() <-
<-![]() ,?
,?
即4![]() +
+![]() <1,两边平方,得
<1,两边平方,得
16-16a+9-24a+8![]() <1,??
<1,??
8![]() <40a-24,?
<40a-24,?
即![]() <5a-3.③?
<5a-3.③?
当a<![]() 时,5a-3<0,从而不等式③无解.?
时,5a-3<0,从而不等式③无解.?
下面再解x4<x1的情形,即?
![]() <-2-2
<-2-2![]() ,?
,?
-3+![]() <-4-4
<-4-4![]() ,有
,有![]() <-1-4
<-1-4![]() .?④?
.?④?
显然,不等式④无解.?
结合以上各式可知,不存在满足题目要求的a.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目