题目内容
已知函数 .
.(1)若
 ,且
,且 时,求:函数f(x)的值;
时,求:函数f(x)的值;(2)若
 时,求:函数f(x)的最大值与最小值;
时,求:函数f(x)的最大值与最小值;(3)用“五点法”画出函数f(x)在[0,π]上的图象.
【答案】分析:(1)化简函数f(x)的解析式为 (sin2x+cos2x),由
(sin2x+cos2x),由 ,且
,且 ,求出 sinx和cosx 的值,再
,求出 sinx和cosx 的值,再
利用二倍角公式可得sin2x和cos2x的值,即得f(x)的值.
(2)由(1)得 ,若
,若 时,x+
时,x+ ∈[
∈[ ,
, ],当x+
],当x+ =
= 时,函数f(x)有最大值为2,当x+
时,函数f(x)有最大值为2,当x+ =
= 时,函数f(x)有最小值-
时,函数f(x)有最小值- .
.
(3)函数f(x)的周期为π,列表,描点作图,即得所求.
解答:解:(1) =
= (sin2x+cos2x). 由
(sin2x+cos2x). 由 ,且
,且 ,
,
可得 sinx= ,cosx=
,cosx= ,∴sin2x=2sinxcosx=-
,∴sin2x=2sinxcosx=- ,cos2x=2cos2x-1=
,cos2x=2cos2x-1= ,
,
所以: .
.
(2)由(1)得: ,若
,若 时,x+
时,x+ ∈[
∈[ ,
, ],
],
∴当x+ =
= 时,函数f(x)有最大值为2,当x+
时,函数f(x)有最大值为2,当x+ =
= 时,函数f(x)有最小值为 2×
时,函数f(x)有最小值为 2× =-
=- .
.
(3)函数f(x)的周期为π,列表
如图:

点评:本题考查三角函数的恒等变换及化简求值,求三角函数的最值,用五点法做出y=Asin(ωx+∅)在一个周期内的简图,
化简函数f(x)的解析式,是解题的突破口.
 (sin2x+cos2x),由
(sin2x+cos2x),由 ,且
,且 ,求出 sinx和cosx 的值,再
,求出 sinx和cosx 的值,再利用二倍角公式可得sin2x和cos2x的值,即得f(x)的值.
(2)由(1)得
 ,若
,若 时,x+
时,x+ ∈[
∈[ ,
, ],当x+
],当x+ =
= 时,函数f(x)有最大值为2,当x+
时,函数f(x)有最大值为2,当x+ =
= 时,函数f(x)有最小值-
时,函数f(x)有最小值- .
.(3)函数f(x)的周期为π,列表,描点作图,即得所求.
解答:解:(1)
 =
= (sin2x+cos2x). 由
(sin2x+cos2x). 由 ,且
,且 ,
,可得 sinx=
 ,cosx=
,cosx= ,∴sin2x=2sinxcosx=-
,∴sin2x=2sinxcosx=- ,cos2x=2cos2x-1=
,cos2x=2cos2x-1= ,
,所以:
 .
.(2)由(1)得:
 ,若
,若 时,x+
时,x+ ∈[
∈[ ,
, ],
],∴当x+
 =
= 时,函数f(x)有最大值为2,当x+
时,函数f(x)有最大值为2,当x+ =
= 时,函数f(x)有最小值为 2×
时,函数f(x)有最小值为 2× =-
=- .
.(3)函数f(x)的周期为π,列表
2x+ |  | π |  | 2π | |
| x | - |  |  |  |  |
| y | 2 | -2 |

点评:本题考查三角函数的恒等变换及化简求值,求三角函数的最值,用五点法做出y=Asin(ωx+∅)在一个周期内的简图,
化简函数f(x)的解析式,是解题的突破口.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
 ,
,
 ,求
,求 的单调区间;
的单调区间; 时,求证:
时,求证: .
.
 .
. 为
为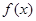 的极值点,求实数
的极值点,求实数 的值;
的值; 在
在 上为增函数,求实数
上为增函数,求实数 时,方程
时,方程 有实根,求实数
有实根,求实数 的最大值.
的最大值. 。
。 ,求函数
,求函数 的值;
的值; .
.
 中任取一个元素
中任取一个元素 ,从集合
,从集合 中任取一个元素
中任取一个元素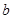 ,求方程
,求方程 有两个不相等实根的概率;
有两个不相等实根的概率; 中任取的一个数,
中任取的一个数, 中任取的一个数,求方程
中任取的一个数,求方程