Question

若实数x、y满足等式(x－2)²＋y²＝3，那么的最大值为

A.                                                              B.

C.                                                            D.

Answer 1

解法一:∵实数x、y满足(x－2)²＋y²＝3，

∴(x，y)是圆(x－2)²＋y²＝3上的点，记为P.

∵是直线OP的斜率，记为k,∴OP:y=kx，代入圆方程，消去y，得(1＋k²)x²－4x＋1=0.直线OP与圆有公共点的充要条件是Δ=(－4)²－4(1＋k²)≥0.

∴－≤k≤.

解法二:同解法一，直线OP与圆有公共点的充要条件是≤，

∴－≤k≤.故选D.

解法三:同解法一，直线OP与圆相切时，k取最值.∴= .∴k=±.

∴k_最大值=.选D.

解法四:方程(x－2)²＋y²＝3的一个参数方程是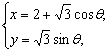设u=，

则u=.∴sinθ－ucosθ=2u，

sin(θ－)＝2u(tan＝u)，

sin(θ－)=.

∵|sin(θ－)|≤1，

∴4u²≤3(1＋u²)，－≤u≤.

∴的最大值为u_最大值=.

答案:D

点评:前三种解法中，利用的几何意义是解决本题的关键.解法四是利用了圆的参数方程及三角函数的值域.解法四中也可利用万能公式，把u表示成tan的函数来求最值.