题目内容
2.已知函数$f(x)=sin(2x+\frac{π}{4})+cos(2x-\frac{π}{4}),x∈R$.(1)求$f(\frac{π}{2})$的值;
(2)求函数f(x)的值域和单调递增区间.
分析 (1)首先利用三角函数的恒等变换把函数的关系式变性成正弦型函数,进一步求出函数的值.
(2)利用正弦型函数的解析式,进一步利用函数的定义域求出函数的值域,最后利用整体思想求出函数的单调区间.
解答 解:(1)$f(x)=sin(2x+\frac{π}{4})+cos(2x-\frac{π}{4})$
=2($\frac{\sqrt{2}}{2}sin2x+\frac{\sqrt{2}}{2}cos2x$)
=2sin(2x+$\frac{π}{4}$),
所以:f($\frac{π}{2}$)=2sin(π+$\frac{π}{4}$)=-$\sqrt{2}$.
(2)由于:x∈R,且f(x)=2sin(2x+$\frac{π}{4}$),
所以函数的值域为:f(x)∈[-2,2].
令:$-\frac{π}{2}+2kπ≤2x+\frac{π}{4}≤2kπ+\frac{π}{2}$
整理得:$-\frac{3π}{8}+kπ≤x≤kπ+\frac{π}{8}$,(k∈Z)
所以函数的单调递增区间为:[$-\frac{3π}{8}+kπ,kπ+\frac{π}{8}$](k∈Z)
点评 本题考查的知识要点:三角函数的关系式的恒等变换,利用正弦型函数的定义域求函数的值域,利用整体思想求函数的单调区间.主要考查学生的应用能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.复数z1,z2在复平面内对应的点关于原点对称,若z1z2=-2i,则|z1|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
10.为了了解潮州市居民月用电情况,抽查了该市100户居民月用电量(单位:度),得到频率分布直方图如下:根据下图可得这100户居民月用电量在〔150,300〕的用户数是( )

| A. | 70 | B. | 64 | C. | 48 | D. | 30 |
7.图中的三个直角三角形是一个体积为30cm3的几何体的三视图,则侧视图中的h为( )


| A. | 5 cm | B. | 6 cm | C. | 7 cm | D. | 8 cm |
14.一个四棱锥的三视图如图所示,那么这个四棱锥的表面积是( )
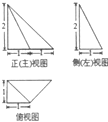

| A. | $\frac{{9+2\sqrt{3}+\sqrt{5}}}{2}$ | B. | $\frac{{9+2\sqrt{3}}}{2}$ | C. | $\frac{{9+2\sqrt{5}}}{2}$ | D. | $\frac{{11+\sqrt{5}}}{2}$ |
14.在等腰△ABC中,∠BAC=90°,AB=AC=2,$\overrightarrow{BC}=2\overrightarrow{BD}$,$\overrightarrow{AC}=3\overrightarrow{AE}$,则$\overrightarrow{AD}•\overrightarrow{BE}$的值为( )
| A. | $-\frac{4}{3}$ | B. | $-\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{4}{3}$ |