题目内容
已知sin22α+sin2αcosα-cos2α=1,α∈(0,
解:方法一:由倍角公式,sin2α=2sinαcosα,cos2α=2cos2α-1,则原式得
4sin2αcos2α+2sinαcos2α-2cos2α=0?2cos2α(2sin2α+sinα-1)=0?2cos2α(2sinα-1)·(sinα+1)=0.∵α∈(0,![]() ),∴sinα+1≠0,cos2α≠0.∴2sinα-1=0,即sinα=
),∴sinα+1≠0,cos2α≠0.∴2sinα-1=0,即sinα=![]() .∴α=
.∴α=![]() .∴tanα=
.∴tanα=![]() .
.
方法二:由题设,得sin22α+sin2αcosα-2cos2α=0,即(sin2α+2cosα)(sin2α-cosα)=0.
∵α∈(0,![]() ),∴sin2α+2cosα≠0.∴sin2α-cosα=0.
),∴sin2α+2cosα≠0.∴sin2α-cosα=0.
∵cosα≠0,∴2sinα-1=0,即sinα=![]() .∴α=
.∴α=![]() .∴tanα=
.∴tanα=![]() .
.
方法三:由题设,得sin22α+sin2αcosα-2cos2α=0,将其看成关于sin2α的一元二次方程,得sin2α=![]() ,
,
∴sin2α=-2cosα或sin2α=cosα.
∵α∈(0,![]() ),∴sin2α≠-2cosα.∴sin2α=cosα(以下同方法二).
),∴sin2α≠-2cosα.∴sin2α=cosα(以下同方法二).
点评:本题是考查三角函数的综合题,能抓住“二倍角公式”和“同角三角函数关系式”这两个知识重点,把它们有机地组合在一起.解题过程运用“换元法”等基本数学方法,体现方程思想,在考查基础知识的基本技能的同时达到考查数学思想方法的目标.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 ),求sin α、tan α的值.
),求sin α、tan α的值.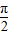 ),求sin α、tan α的值.
),求sin α、tan α的值.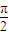 ),求sin α、tan α的值.
),求sin α、tan α的值.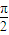 ),求sin α、tan α的值.
),求sin α、tan α的值.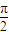 ),求sin α、tan α的值.
),求sin α、tan α的值.