题目内容
已知sin22α+sin 2αcos α-cos 2α=1,α∈(0,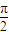 ),求sin α、tan α的值.
),求sin α、tan α的值.
【答案】分析:利用平方关系直接化简sin22α+sin 2αcos α-cos 2α=1,根据正弦函数的有界性,求出sinα= ,然后求出tan α的值即可.
,然后求出tan α的值即可.
解答:解:由sin22α+sin2αcosα-cos2α=1,得
4sin2αcos2α+2sinαcos2α-2cos2α=0
2cos2α(2sin2α+sinα-1)=0
2cos2α(2sinα-1)(sinα+1)=0.
因为α∈(0, ),所以sinα+1≠0,且cosα≠0,
),所以sinα+1≠0,且cosα≠0,
所以2sinα-1=0,即sinα= ,
,
所以α= ,即tanα=
,即tanα= .
.
点评:本题考查同角三角函数的基本关系式的应用,考查计算能力,是基础题.
 ,然后求出tan α的值即可.
,然后求出tan α的值即可.解答:解:由sin22α+sin2αcosα-cos2α=1,得
4sin2αcos2α+2sinαcos2α-2cos2α=0
2cos2α(2sin2α+sinα-1)=0
2cos2α(2sinα-1)(sinα+1)=0.
因为α∈(0,
 ),所以sinα+1≠0,且cosα≠0,
),所以sinα+1≠0,且cosα≠0,所以2sinα-1=0,即sinα=
 ,
,所以α=
 ,即tanα=
,即tanα= .
.点评:本题考查同角三角函数的基本关系式的应用,考查计算能力,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ),求sin α、tan α的值.
),求sin α、tan α的值.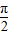 ),求sin α、tan α的值.
),求sin α、tan α的值.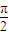 ),求sin α、tan α的值.
),求sin α、tan α的值.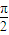 ),求sin α、tan α的值.
),求sin α、tan α的值.