题目内容
已知函数f(x)=x2+ax+b(a,b∈R)的值域为[0,+∞),若关于x的不等式f(x)<c的解集为(0,6),则实数c=( )A.9
B.8
C.7
D.6
【答案】分析:由题意函数f(x)=x2+ax+b,(a,b∈R)的值域为[0,+∞),可得△=0,再根据不等式f(x)<c的解集为(0,6),说明f(x)-c=0的两个根为0和6,代入得两个式子,可以解出c值.
解答:解:∵函数f(x)=x2+ax+b,(a,b∈R)的值域为[0,+∞),
∴△=a2-4b=0…①,
∵关于x的不等式f(x)<c的解集为(0,6),
∴方程x2+ax+b-c=0的两个根为0和6,
∴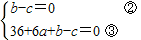
由①②③可以解得:a=-6,b=9,c=9;
故选A.
点评:本题主要考查了二次函数的性质,方程根与系数的关系一直是高考的热点问题,此题难度不大,是一道基础题.
解答:解:∵函数f(x)=x2+ax+b,(a,b∈R)的值域为[0,+∞),
∴△=a2-4b=0…①,
∵关于x的不等式f(x)<c的解集为(0,6),
∴方程x2+ax+b-c=0的两个根为0和6,
∴
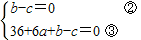
由①②③可以解得:a=-6,b=9,c=9;
故选A.
点评:本题主要考查了二次函数的性质,方程根与系数的关系一直是高考的热点问题,此题难度不大,是一道基础题.

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|