题目内容
已知正四棱柱 中,
中, 是
是 的中点.
的中点.
(I)求证: 平面
平面 ;
;
(II)求证: ;
;
(III)在线段 上是否存在点
上是否存在点 ,当
,当 时,平面
时,平面 平面
平面 ?若存在,求出
?若存在,求出 的值并证明;若不存在,请说明理由.
的值并证明;若不存在,请说明理由.

解:(Ⅰ)在正四棱柱 中,连结
中,连结 交
交 于
于 ,连结
,连结 .
.
因为 为正方形,
为正方形,
所以 为
为 中点.
中点.
在 中,
中,
因为 为
为 中点,
中点,
所以 ∥
∥ .
.
因为
 平面
平面 ,
,
 平面
平面 ,
,
所以 ∥平面
∥平面 .
.
 (Ⅱ) 因为
(Ⅱ) 因为 为正方形,
为正方形,
所以 .
.
因为 平面
平面 ,
,
所以 .
.
因为 ,
,
所以 平面
平面 .
.
因为 ,
,
所以 .
.
(Ⅲ)当 ,即点
,即点 为线段
为线段 的中点时,平面
的中点时,平面 平面
平面
因为 且
且 ,
,
所以四边形 是平行四边形.
是平行四边形.
所以 .
.
取 的中点
的中点 ,连结
,连结 .
.
因为 为
为 中点,
中点,
所以 且
且 ,
,
所以四边形 是平行四边形.
是平行四边形.
所以 .
.
同理 .
.
所以 .
.
因为 ,
, ,
,
所以平面 平面
平面 .
.

练习册系列答案
相关题目
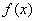 的图象大致是( )
的图象大致是( )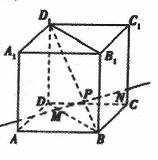
 其中
其中 表示不超过
表示不超过 的最大整数,
的最大整数, ,
, ,
, ).若直线
).若直线 与函数
与函数 的图象恰有三个不同的交点,则实数
的图象恰有三个不同的交点,则实数 的取值范围是
的取值范围是  B.
B. C.
C.  D.
D.
 (B)
(B) (C)
(C) (D)
(D)


 的不等式
的不等式 的解集为
的解集为 ,则实数
,则实数 的值分别为( )
的值分别为( )



 在
在 内有极小值的充分不必要条件是( )
内有极小值的充分不必要条件是( )



 ,已知
,已知 ,那么△ABC一定是
,那么△ABC一定是  的图像,只需将函数
的图像,只需将函数 的图像( )
的图像( ) 个单位长度 B.向右平行移动
个单位长度 B.向右平行移动 个单位长度 D.向右平行移动
个单位长度 D.向右平行移动