题目内容

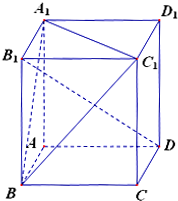
已知点H在正方体ABCD-A′B′C′D′的对角线B′D′上，∠HDA=60°．
（Ⅰ）求DH与CC′所成角的大小；
（Ⅱ）求DH与平面AA′D′D所成角的大小．
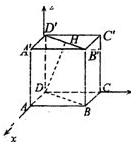
（Ⅰ）建立如图所示的坐标系，设H（m，m，1）（m＞0），则
DA
=（1，0，0），
CC′
=（0，0，1），连接BD，B′D′．
则
DH
=（m，m，1）（m＞0），
由已知＜
DA
，
DH
＞=60°，根据
DA
•
DH
=|
DA
||
DH
|cos＜
DA
，
DH
＞，可得2m=
2m2+1
，解得m=
2
2
，
∴
DH
=（
2
2
，
2
2
，1），
∴cos＜
DA
，
CC′
＞=
2
2
，
∴＜
DA
，
CC′
＞=45°，即DH与CC′所成角的大小为45°；
（Ⅱ）平面AA′D′D的一个法向量为
DC
=（0，1，0），
∴cos＜
DH
，
DC
＞=
0+
2
2
+0
2
=
1
2
，
∴＜
DH
，
DC
＞=60°，
∴DH与平面AA′D′D所成角的大小为30°．
练习册系列答案
相关题目
如果两个相交平面都垂直于第三个平面，那么它们的交线也垂直于这个平面。
已知：β⊥α，γ⊥α，βγ=a
求证：a⊥α
如图所示，正三棱柱ABC-A1B1C1的底面边长是2，侧棱长是
3
，D是AC的中点．
（Ⅰ）求证：B1C∥平面A1BD；
（Ⅱ）求二面角A1-BD-A的大小；
（Ⅲ）求点A到平面A1BD的距离．
如图，在棱长为1的正方体A1B1C1D1-ABCD中，
（1）求直线B1D与平面A1BC1所成的角；
（2）求点A到面A1BC1的距离．
如图，正三棱柱ABC-A1B1C1所有棱长都是2，D是棱AC的中点，E是棱CC1的中点，AE交A1D于点H．
（1）求证：AE⊥平面A1BD；
（2）求二面角D-BA1-A的大小（用反三角函数表示）
（3）求点B1到平面A1BD的距离．
如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠BAD=60°，Q为AD的中点，PA=PD=AD=2．
（Ⅰ）求证：AD⊥平面PQB；
（Ⅱ）点M在线段PC上，PM=tPC，试确定t的值，使PA∥平面MQB；
（Ⅲ）若PA∥平面MQB，平面PAD⊥平面ABCD，求二面角M-BQ-C的大小．
如图，在长方体ABCD-A1B1C1D1中AA1=AD=1，E为CD中点．
（1）在棱AA1上是否存在一点P，使得DP∥平面B1AE？若存在，求AP的长；若不存在，说明理由．
（2）若二面角A-B1E-A1的大小为30°，求AB的长．
在四棱锥P-ABCD中，PA⊥平面ABCD，△ABC是正三角形，AC与BD的交点M恰好是AC中点，又PA=AB=4，∠CDA=120°．
（1）求证：BD⊥PC；
（2）设E为PC的中点，点F在线段AB上，若直线EF∥平面PAD，求AF的长；
（3）求二面角A-PC-B的余弦值．
如图，直三棱柱ABC-A1B1C1中，CA⊥CB，CA=CB=1，棱AA1=2，M、N分别是A1B1、A1A的中点．
（1）求证：C1N⊥平面BCN；
（2）求直线B1C与平面C1MN所成角θ的正弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网