题目内容
设函数f(x)=sin(![]() x+
x+![]() )﹣2sin2
)﹣2sin2![]() x.
x.
(1)求函数f(x)的最小正周期;
(2)若函数y=g(x)的图象与函数y=f(x)的图象关于原点对称,求S=g(1)+g(2)+…+g(2012)的值.
考点:
三角函数中的恒等变换应用;函数的值;三角函数的周期性及其求法.
专题:
计算题.
分析:
(1)利用三角函数的恒等变换化简函数f(x)的解析式为 ![]() sin(
sin(![]() x+
x+![]() )﹣1,由此求得f(x)的最小正周期.
)﹣1,由此求得f(x)的最小正周期.
(2)在函数y=g(x)的图象上任取一点(x,g(x)),则它关于原点的对称点(﹣x,﹣g(x))在函数y=f(x)的图象上,由此求得 g(x)=![]() sin(
sin(![]() x﹣
x﹣![]() )+1,由此求得
)+1,由此求得
函数g(x)的周期为4,求出g(1)+g(2)+g(3)+g(4)的值,即可求得S=g(1)+g(2)+…+g(2012)的值.
解答:
解:(1)∵函数f(x)=sin(![]() x+
x+![]() )﹣2sin2
)﹣2sin2![]() x=
x=![]() sin
sin![]() x+
x+![]() cos
cos![]() x﹣2•
x﹣2•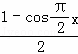
=![]() (
(![]() sin
sin![]() x+
x+![]() cos
cos![]() x)﹣1=
x)﹣1=![]() sin(
sin(![]() x+
x+![]() )﹣1,
)﹣1,
故函数f(x)的最小正周期T=![]() =4.
=4.
(2)∵函数y=g(x)的图象与函数y=f(x)的图象关于原点对称,在函数y=g(x)的图象上任取一点
(x,g(x)),则它关于原点的对称点(﹣x,﹣g(x))在函数y=f(x)的图象上,
即点(﹣x,﹣g(x))的坐标满足函数y=f(x)的解析式,故有﹣g(x)=![]() sin(﹣
sin(﹣![]() x+
x+![]() )﹣1=﹣
)﹣1=﹣![]() sin(
sin(![]() x﹣
x﹣![]() )﹣1,
)﹣1,
∴g(x)=![]() sin(
sin(![]() x﹣
x﹣![]() )+1,故函数g(x)的周期为4.
)+1,故函数g(x)的周期为4.
∵g(1)=![]() sin(
sin(![]() ﹣
﹣![]() )+1=
)+1=![]() +1,g(2)=
+1,g(2)=![]() sin(
sin(![]() ×2﹣
×2﹣![]() )+1=
)+1=![]() +1,g(3)=
+1,g(3)=![]() sin(
sin(![]() ×3﹣
×3﹣![]() )+1=1﹣
)+1=1﹣![]() ,
,
g(4)=![]() sin(
sin(![]() ×4﹣
×4﹣![]() )+1=1﹣
)+1=1﹣![]() ,∴g(1)+g(2)+g(3)+g(4)=4.
,∴g(1)+g(2)+g(3)+g(4)=4.
S=g(1)+g(2)+…+g(2012)=503(g(1)+g(2)+g(3)+g(4))=503×4=2012.
点评:
本题主要考查三角函数的恒等变换及化简求值,利用函数的周期性求函数值,属于中档题.

 阅读快车系列答案
阅读快车系列答案