题目内容
设集合A={x|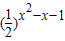
＜1}，B={x|log4（x+a）＜1}，若A∩B=∅，则实数a的取值范围是 ．
【答案】分析：利用指数不等式可求得集合A，利用对数不等式可求得集合B，A∩B=∅，从而可求得实数a的取值范围．
解答：解：∵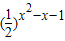
＜1=
，
∴x2-x-1＞0，
∴x＞
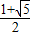或x＜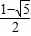
．
∴A={x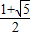|x＞
或x＜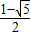
}；
又由log4（x+a）＜1得：0＜x+a＜4，
∴-a＜x＜4-a，
∴B={x|-a＜x＜4-a}；
∵A∩B=∅，
∴
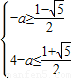，a∈∅
故答案为：∅．
点评：本题考查指、对数不等式的解法，求得集合A与B是关键，考查分析与运算能力，属于中档题．
解答：解：∵
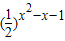＜1=，∴x2-x-1＞0，
∴x＞
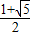或x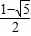＜．∴A={x|x＞
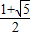或x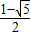＜}；又由log4（x+a）＜1得：0＜x+a＜4，
∴-a＜x＜4-a，
∴B={x|-a＜x＜4-a}；
∵A∩B=∅，
∴
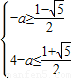，a∈∅故答案为：∅．
点评：本题考查指、对数不等式的解法，求得集合A与B是关键，考查分析与运算能力，属于中档题．
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
设集合A={x|
＜0}，B={x|x-2＜2}那么“m∈A”是“m∈B”（ ）
| x |
| x-1 |
| A、充分而不必要条件 |
| B、必要而不充分 |
| C、充要条件 |
| D、既不充分也不必要条件 |