题目内容
下列命题中:
①arcsin(-
)=-
②arccos(-
)=
③arctan
=
④arccos1=0,
其中正确的命题的个数有( )
①arcsin(-
| 1 |
| 2 |
| π |
| 6 |
②arccos(-
| 1 |
| 2 |
| 2π |
| 3 |
③arctan
| ||
| 3 |
| π |
| 6 |
④arccos1=0,
其中正确的命题的个数有( )
分析:利用反三角函数的概念与性质即可得到答案.
解答:解:①∵y=arcsinx∈[-
,
],sin[arcsin(-
)]=-
,
∴arcsin(-
)=-
,故①正确;
②y=arccosx∈[0,π],cos[arccos(-
)]=-
,
∴arccos(-
)=
,故②正确;
同理可知④正确;
对于③,y=arctanx∈(-
,
),tan(arctan
)=
,
当x∈(-
,
)时,tan
=
,
∴arctan
=
,正确.
故选D.
| π |
| 2 |
| π |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴arcsin(-
| 1 |
| 2 |
| π |
| 6 |
②y=arccosx∈[0,π],cos[arccos(-
| 1 |
| 2 |
| 1 |
| 2 |
∴arccos(-
| 1 |
| 2 |
| 2π |
| 3 |
同理可知④正确;
对于③,y=arctanx∈(-
| π |
| 2 |
| π |
| 2 |
| ||
| 3 |
| ||
| 3 |
当x∈(-
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
| ||
| 3 |
∴arctan
| ||
| 3 |
| π |
| 6 |
故选D.
点评:本题考查反三角函数的运用,考查命题的真假判断与应用,属于中档题.

练习册系列答案
相关题目
 ,则
,则 ;
;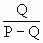 ;
;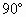 .
.