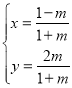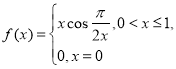Question

【题目】已知非空集合是由一些函数组成，满足如下性质：①对任意，均存在反函数，且；②对任意，方程均有解；③对任意、，若函数为定义在上的一次函数，则.

（1）若，，均在集合中，求证：函数；

（2）若函数（）在集合中，求实数的取值范围；

（3）若集合中的函数均为定义在上的一次函数，求证：存在一个实数，使得对一切，均有.

Answer 1

【答案】（1）见详解；（2）；（3）见详解；

【解析】

（1）由，根据性质①可得，且存在，使得

，由，且为一次函数，根据性质③即可证明.

（2）由性质②，方程，即在上有解，可得，

变形，.对与的关系分类讨论，利用基本不等式的性质即可求解.

（3）任取，，由性质①，不妨设，

（若，则，），

由性质③函数，

由性质①：，

由性质③：

由性质②方程：，可得，即，即可得证.

（1）由，根据性质①可得，且存在，使得

，由，且为一次函数，

根据性质③可得：.

（2）由性质②，方程，即在上有解，，

由,

若，时，，且，

此时没有反函数，即不满足性质①.

若，时，函数在上单调递增，此时有反函数，

即满足性质①.

综上：.

（3）任取，，由性质①，不妨设，

（若，则，），

由性质③函数，

由性质①：，

由性质③：

由性质②方程：，

，即，

，可得，,

，可得，,

由此可知：对于任意两个函数，，

存在相同的满足：，

存在一个实数，使得对一切，均有.