题目内容
P为双曲线
上的一点，F为一个焦点，以PF为直径的圆与圆x2+y2=a2的位置关系是( ) A.内切 B.内切或外切 C.外切 D.相离或相交
提示：设|PF|的中点为M，F1为另一焦点，则在△F1PF中，|OM|=
|PF1|=
(2a±|PF|)=a±
|PF|,即圆心距等于两圆半径之和或差.
答案：B
练习册系列答案
53天天练系列答案
相关题目
已知F1、F2分别是双曲线
-
=1（a＞0，b＞0）的左、右焦点，P为双曲线上的一点，若∠F1PF2=90°，且△F1PF2的三边长成等差数列，则双曲线的离心率是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、2 | B、3 | C、4 | D、5 |
已知F1、F2分别是双曲线
-
=1(b＞0)的左、右焦点，P为双曲线上的一点，若∠F1PF2=120°，且△F1PF2的三边长成等差数列，则双曲线的渐近线的斜率是（ ）
| x2 |
| 4 |
| y2 |
| b2 |
A、±
| ||||
B、±
| ||||
C、±
| ||||
D、±
|
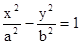（a>0,b>0）的左、右焦点，P为双曲线上的一点，若
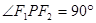,且
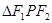的三边长成等差数列，则双曲线的离心率是（
）