题目内容
 已知f(x)=
已知f(x)=
| ||
|
(1)判断f(x)的奇偶性;
(2)当x∈[-π,π]时,画出f(x)的简图,并指出函数的单调区间.
分析:(1)由已知中f(x)=
,我们可以先求出函数的定义域A,验证A是否关于原点对称,若对称,再判断f(-x)与f(x)的关系,然后根据函数奇偶性的定义得到结论.
(2)根据(1)中函数的解析式,我们结合正切函数的图象及函数的对折变换及画出当x∈[-π,π]时,画出f(x)的简图,结合函数的图象即可得到函数的单调区间.
| ||
|
(2)根据(1)中函数的解析式,我们结合正切函数的图象及函数的对折变换及画出当x∈[-π,π]时,画出f(x)的简图,结合函数的图象即可得到函数的单调区间.
解答:解:(1)由函数f(x)=
的解析式可得
函数的定义域为{x|x≠kπ+
,k∈Z}关于原点对称
又∵f(x)=
=
∴f(-x)=
=-
=-f(x)
∴函数f(x)=
为奇函数..(4分)
(2)由(1)可得f(x)=
其图象如下图所示:
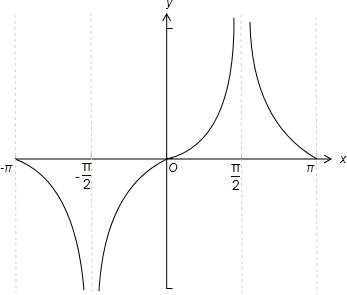
由图可知函数f(x)=
在(-
,
)递增,在[-π,-
)及(
,π]递减
| ||
|
函数的定义域为{x|x≠kπ+
| π |
| 2 |
又∵f(x)=
| ||
|
| sinx |
| |cosx| |
∴f(-x)=
| sin(-x) |
| |cos(-x)| |
| sinx |
| |cosx| |
∴函数f(x)=
| ||
|
(2)由(1)可得f(x)=
|
其图象如下图所示:

由图可知函数f(x)=
| ||
|
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
点评:本题考查的知识点是正切函数的图象,函数奇偶性的判断,正切函数的单调性,(1)中一定要先判断函数的定义域A是否关于原点对称,(2)中关键是要将函数的解析式化为分段函数的形式.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目