题目内容
已知直线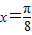 是函数f(x)=sin(2x+ϕ)(-π<ϕ<0)图象的一条对称轴.有以下几个结论:
是函数f(x)=sin(2x+ϕ)(-π<ϕ<0)图象的一条对称轴.有以下几个结论:①
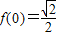 ;
;②
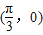 是f(x)图象的一个对称中心;
是f(x)图象的一个对称中心;③
 是f(x)的一个单调增区间;
是f(x)的一个单调增区间;④将f(x)的图象向左平移
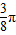 个单位长度,即得到函数y=sin2x的图象.
个单位长度,即得到函数y=sin2x的图象.其中正确结论的序号是 .(将你认为正确的结论的序号都填上)
【答案】分析:根据对称轴及∅的范围,求出∅值,得到函数f(x)=sin(2x- ),求出f(0)=sin(-
),求出f(0)=sin(- )=-
)=- ,故①不正确.
,故①不正确.
当 x= 时,f(
时,f( )=sin(-
)=sin(- )≠0,故②不正确.
)≠0,故②不正确.
由 2kπ- ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z,可得
,k∈z,可得  是f(x)的一个单调增区间,故③正确.
是f(x)的一个单调增区间,故③正确.
将f(x)的图象向左平移 个单位长度,即得到函数y=sin[2(x+
个单位长度,即得到函数y=sin[2(x+ )-
)- ]=sin2x,故④正确.
]=sin2x,故④正确.
解答:解:由题意可得 时,函数f(x)=sin(2x+ϕ)=sin(
时,函数f(x)=sin(2x+ϕ)=sin( +∅)取得最值,故 (
+∅)取得最值,故 ( +∅)=kπ+
+∅)=kπ+ ,k∈z,
,k∈z,
∴∅=kπ+ .再由-π<ϕ<0,可得∅=-
.再由-π<ϕ<0,可得∅=- .∴函数f(x)=sin(2x+ϕ)=sin(2x-
.∴函数f(x)=sin(2x+ϕ)=sin(2x- ).
).
∴f(0)=sin(- )=-
)=- ,故①不正确.
,故①不正确.
当 x= 时,f(
时,f( )=sin(-
)=sin(- )≠0,故②不正确.
)≠0,故②不正确.
由 2kπ- ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z,可得 kπ+
,k∈z,可得 kπ+ ≤x≤kπ+
≤x≤kπ+ ,∴
,∴ 是f(x)的一个单调增区间,
是f(x)的一个单调增区间,
故③正确.
将f(x)的图象向左平移 个单位长度,即得到函数y=sin[2(x+
个单位长度,即得到函数y=sin[2(x+ )-
)- ]=sin2x,故④正确.
]=sin2x,故④正确.
故答案为:③④.
点评:本题考查正弦函数的单调性,对称性,y=Asin(ωx+∅)图象的变换,掌握正弦函数的图象性质,是解题的关键.
 ),求出f(0)=sin(-
),求出f(0)=sin(- )=-
)=- ,故①不正确.
,故①不正确.当 x=
 时,f(
时,f( )=sin(-
)=sin(- )≠0,故②不正确.
)≠0,故②不正确.由 2kπ-
 ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z,可得
,k∈z,可得  是f(x)的一个单调增区间,故③正确.
是f(x)的一个单调增区间,故③正确.将f(x)的图象向左平移
 个单位长度,即得到函数y=sin[2(x+
个单位长度,即得到函数y=sin[2(x+ )-
)- ]=sin2x,故④正确.
]=sin2x,故④正确.解答:解:由题意可得
 时,函数f(x)=sin(2x+ϕ)=sin(
时,函数f(x)=sin(2x+ϕ)=sin( +∅)取得最值,故 (
+∅)取得最值,故 ( +∅)=kπ+
+∅)=kπ+ ,k∈z,
,k∈z,∴∅=kπ+
 .再由-π<ϕ<0,可得∅=-
.再由-π<ϕ<0,可得∅=- .∴函数f(x)=sin(2x+ϕ)=sin(2x-
.∴函数f(x)=sin(2x+ϕ)=sin(2x- ).
).∴f(0)=sin(-
 )=-
)=- ,故①不正确.
,故①不正确.当 x=
 时,f(
时,f( )=sin(-
)=sin(- )≠0,故②不正确.
)≠0,故②不正确.由 2kπ-
 ≤2x-
≤2x- ≤2kπ+
≤2kπ+ ,k∈z,可得 kπ+
,k∈z,可得 kπ+ ≤x≤kπ+
≤x≤kπ+ ,∴
,∴ 是f(x)的一个单调增区间,
是f(x)的一个单调增区间,故③正确.
将f(x)的图象向左平移
 个单位长度,即得到函数y=sin[2(x+
个单位长度,即得到函数y=sin[2(x+ )-
)- ]=sin2x,故④正确.
]=sin2x,故④正确.故答案为:③④.
点评:本题考查正弦函数的单调性,对称性,y=Asin(ωx+∅)图象的变换,掌握正弦函数的图象性质,是解题的关键.

练习册系列答案
相关题目
 是函数f(x)=sin(2x+?)(-π<?<0)图象的一条对称轴.有以下几个结论:
是函数f(x)=sin(2x+?)(-π<?<0)图象的一条对称轴.有以下几个结论: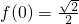 ;
; 是f(x)图象的一个对称中心;
是f(x)图象的一个对称中心;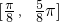 是f(x)的一个单调增区间;
是f(x)的一个单调增区间;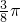 个单位长度,即得到函数y=sin2x的图象.
个单位长度,即得到函数y=sin2x的图象.