题目内容
(本小题满分12分)已知函数 .
.
(1)讨论 的单调性;
的单调性;
(2)设 ,证明:当
,证明:当 时,
时, ;
;
(3)若函数 的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,
的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,
证明: (x0)<0.
(x0)<0.
 .
.(1)讨论
 的单调性;
的单调性;(2)设
 ,证明:当
,证明:当 时,
时, ;
;(3)若函数
 的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,
的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明:
 (x0)<0.
(x0)<0.解:
(1)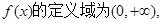
 单调增加,在
单调增加,在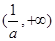 单调减少.
单调减少.
(2)当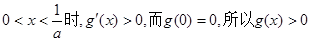 .
.
故当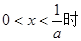 ,
,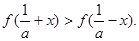
(3)见解析。
(1)
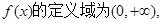
 单调增加,在
单调增加,在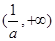 单调减少.
单调减少. (2)当
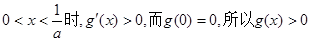 .
.故当
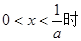 ,
,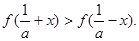
(3)见解析。
本试题主要是考查了导数在研究函数中的运用。求解单调性和及证明不等式等知识的运用。
(1)先求解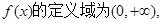 然后求解
然后求解 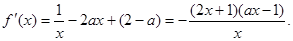
对于参数a分情况讨论得到单调区间。
(2)构造函数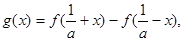 则其导数为
则其导数为
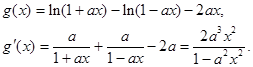
然后分析导数大于零或者小于零的解即可。
(3)由(1)可得,当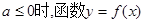 的图像与x轴至多有一个交点,
的图像与x轴至多有一个交点,
故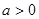 ,从而
,从而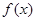 的最大值为
的最大值为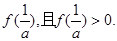 ,这样结合可知分析得到结论。
,这样结合可知分析得到结论。
解:
(1)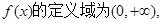
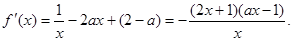
(i)若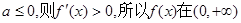 单调增加.
单调增加.
(ii)若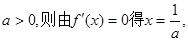 且
且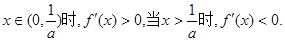
所以 单调增加,在
单调增加,在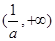 单调减少. ………………4分
单调减少. ………………4分
(2)设函数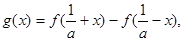 则
则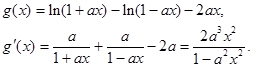
当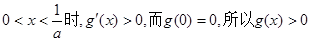 .
.
故当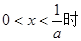 ,
,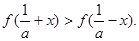 ………………8分
………………8分
(3)由(1)可得,当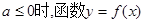 的图像与x轴至多有一个交点,
的图像与x轴至多有一个交点,
故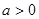 ,从而
,从而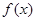 的最大值为
的最大值为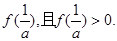 不妨设
不妨设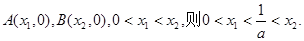 由(2)得
由(2)得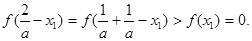 从而
从而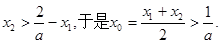
由(I)知, ………………12分
………………12分
(1)先求解
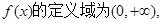 然后求解
然后求解 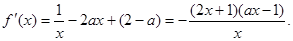
对于参数a分情况讨论得到单调区间。
(2)构造函数
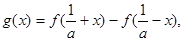 则其导数为
则其导数为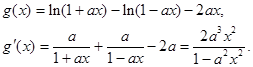
然后分析导数大于零或者小于零的解即可。
(3)由(1)可得,当
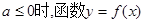 的图像与x轴至多有一个交点,
的图像与x轴至多有一个交点,故
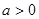 ,从而
,从而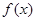 的最大值为
的最大值为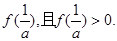 ,这样结合可知分析得到结论。
,这样结合可知分析得到结论。解:
(1)
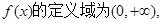
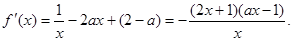
(i)若
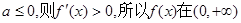 单调增加.
单调增加.(ii)若
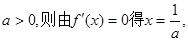 且
且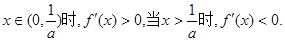
所以
 单调增加,在
单调增加,在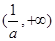 单调减少. ………………4分
单调减少. ………………4分(2)设函数
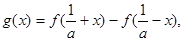 则
则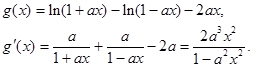
当
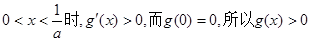 .
.故当
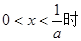 ,
,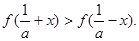 ………………8分
………………8分(3)由(1)可得,当
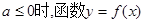 的图像与x轴至多有一个交点,
的图像与x轴至多有一个交点,故
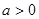 ,从而
,从而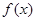 的最大值为
的最大值为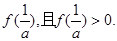 不妨设
不妨设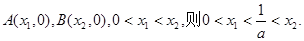 由(2)得
由(2)得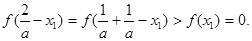 从而
从而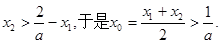
由(I)知,
 ………………12分
………………12分
练习册系列答案
相关题目
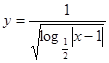 的定义域是 .
的定义域是 .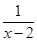 ;
;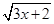 ;
;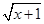 +
+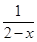 .
. 是函数
是函数 的极大值点,则
的极大值点,则 等于( )
等于( ) ,函数
,函数 定义域中任意的
定义域中任意的 ,有如下结论:
,有如下结论: ; ②
; ② ;
; ④
④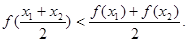
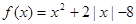 ,定义域为
,定义域为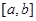
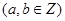 ,值域为
,值域为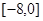 ,则满足条件的整数对
,则满足条件的整数对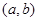 有 对.
有 对. 的定义域为( )
的定义域为( )
 }
} 的定义域是( )
的定义域是( )

