题目内容
已知离心率为
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
-2.
(1)求椭圆的标准方程;
(2)如果直线l:y=kx+m与椭圆相交于P1、P2两点,设直线P1F1与P2F1的倾斜角分别为α,β,当α+β=π时,求证:直线l必过定点.
分析:(1)利用椭圆的离心率的值,得到椭圆中参数的关系,利用椭圆C1与抛物线C2:y2=-x的交点的横坐标为-2,代入抛物线的方程,求出交点的坐标,代入椭圆方程求出参数值,即得到椭圆的方程.
(2)将直线的方程与椭圆的方程联立,利用韦达定理,得到交点的坐标满足的条件,将已知条件α+β=π转化为两条直线的斜率满足k1+k2=0,将斜率用坐标表示,得到 m=4k,代入直线的方程,判断出直线过定点.
(2)将直线的方程与椭圆的方程联立,利用韦达定理,得到交点的坐标满足的条件,将已知条件α+β=π转化为两条直线的斜率满足k1+k2=0,将斜率用坐标表示,得到 m=4k,代入直线的方程,判断出直线过定点.
解答: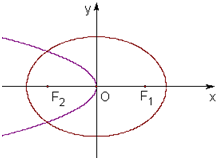 解:(1)由于e2=
解:(1)由于e2=
=1-
=
,
=
,a2=2b2
又因y2=-x的交点的横坐标为-2,y2=2,代入
+
=1,
=1,b2=4,
∴a2=8
所以椭圆方程为
+
=1
(2)联立
+
=1与y=kx+m得到(2k2+1)x2+4mkx+2m2-8=0x1+x2=-
,x1x2=
设直线P1F1与P2F1的倾斜角分别为α,β,
当α+β=π时,若设k1=kP1F1,k2=kP2F1
k1=tanα,k2=tanβ=tan(π-α)=-tanα=-k1,
∴k1+k2=0
k1=
=
,k2=
=
k1+k2=
+
=
=
=
=
=0
所以 m=4k
直线方程为 y=kx+4k=k(x+4),
故直线过定点 (-4,0)
 解:(1)由于e2=
解:(1)由于e2=| c2 |
| a2 |
| b2 |
| a2 |
| 1 |
| 2 |
| b2 |
| a2 |
| 1 |
| 2 |
又因y2=-x的交点的横坐标为-2,y2=2,代入
| (-2)2 |
| 2b2 |
| 2 |
| b2 |
| 4 |
| b2 |
∴a2=8
所以椭圆方程为
| x2 |
| 8 |
| y2 |
| 4 |
(2)联立
| x2 |
| 8 |
| y2 |
| 4 |
| 4mk |
| 2k2+1 |
| 2m2-8 |
| 2k2+1 |
设直线P1F1与P2F1的倾斜角分别为α,β,
当α+β=π时,若设k1=kP1F1,k2=kP2F1
k1=tanα,k2=tanβ=tan(π-α)=-tanα=-k1,
∴k1+k2=0
k1=
| y1 |
| x1+2 |
| kx1+m |
| x1+2 |
| y2 |
| x2+2 |
| kx2+m |
| x2+2 |
k1+k2=
| kx1+m |
| x1+2 |
| kx2+m |
| x2+2 |
| (kx1+m)(x2+2)+(kx2+m)(x1+2) |
| (x1+2)(x2+2) |
=
| 2kx1x2+(2k+m)(x1+x2)+4m |
| (x1+2)(x2+2) |
=
| 2k(2m2-8)+(2k+m)(-4mk)+4m(2k2+1) |
| (x1+2)(x2+2)(2k2+1) |
| -16k+4m |
| (x1+2)(x2+2)(2k2+1) |
所以 m=4k
直线方程为 y=kx+4k=k(x+4),
故直线过定点 (-4,0)
点评:解决直线与圆锥曲线的相交的有关问题,一般的思路是将直线与圆锥曲线方程联立,得到关于应该未知数的方程,利用韦达定理来解决.属于难题,计算量大.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目