题目内容
函数
（x∈[0，π]）的单调递减区间是
- A.
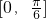
- B.
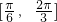
- C.
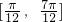
- D.
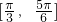
C
分析：利用两角和的正弦公式化简函数f（x）=2sin（2x+
），由 2kπ+
≤2x+≤2kπ+
，k∈z，求得单调减区间，由x∈[0，π]知，进一步确定单调递减区间．
解答：函数=2sin（2x+），
由 2kπ+≤2x+≤2kπ+，k∈z，解得 kπ+
≤x≤kπ+
，k∈z，
故单调减区间为[kπ+，kπ+]，k∈z，
再由x∈[0，π]知，单调递减区间是．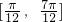
故答案为：．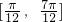
点评：本题主要考查两角和的正弦公式，正弦函数的单调性，得到2kπ+≤2x+≤2kπ+，k∈z，是解题的关键．
分析：利用两角和的正弦公式化简函数f（x）=2sin（2x+
），由 2kπ+≤2x+≤2kπ+，k∈z，求得单调减区间，由x∈[0，π]知，进一步确定单调递减区间．解答：函数
=2sin（2x+），由 2kπ+
≤2x+≤2kπ+，k∈z，解得 kπ+≤x≤kπ+，k∈z，故单调减区间为[kπ+
，kπ+]，k∈z，再由x∈[0，π]知，单调递减区间是
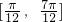．故答案为：
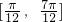．点评：本题主要考查两角和的正弦公式，正弦函数的单调性，得到2kπ+
≤2x+≤2kπ+，k∈z，是解题的关键． 
练习册系列答案
相关题目
函数f（x），g（x）的图象分别如右图1、2所示．函数h（x）=f（x）+g（x）．则以下有关函数h（x）的性质中，错误的是（ ）