Question

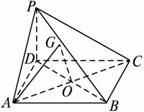
在四棱锥P—ABCD中，底面ABCD是边长为a的正方形，并且PD=a,　PA=PC=a,

       (1)求证：PD⊥平面ABCD；

       (2)求异面直线PB与AC所成的角；

       (3)求二面角A－PB－D的大小；

       (4)在这个四棱锥中放入一个球，求这个球的最大半径.

Answer 1

(1)证明：∵PD=a,PA=PC=a,?

∴△PAD和△PCD都是等腰直角三角形.?

从而PD⊥平面ABCD.?

(2)解析：PB在底面的射影是DB，而DB⊥AC，PD⊥平面ABCD，由三垂线定理得PB⊥AC,∴异面直线PB与AC所成的角为直角.?

(3)解析：设AC与BD相交于O，过O作OG⊥PB于G，连结AG,?

∵AO⊥BD,AO⊥PD,?

∴AO⊥平面PBD.?

由三垂线定理可得∠AGO就是二面角A-PB-D的平面角.?

易得OG=a,AC=,tan∠AGO=,∴∠AGO=arctan,即二面角A-PB-D的大小为arctan.?

(4)解析：∵所求球必与四棱锥内切，?

∴球心到各面的距离均为球半径R，把球心与各顶点连结起来，四棱锥P—ABCD的体积就分成以球心为顶点的五个小三棱锥的体积.?

S_全=S_底+S_侧=a²+(2×a²+2×a×a)=(2+)a².?

又四棱锥P—ABCD的体积为V=a³,?则由V=S_全×R，得R=a.