题目内容
已知数列{an}的前n项和Sn=3n+k(k为常数),那么下述结论正确的是[ ]
A.k为任意实数时,{an}为等比数列 B.k=0时,{an}是等比数列
C.k=-1时,{an}是等比数列 D.{an}不可能成为等比数列
答案:C
解析:
提示:
解析:
|
解: a1=3+k an=2·3n-1 (an = Sn-Sn-1) 3+k=2·31-1 ∴ k=-1 |
提示:
| 注意首项是什么 |

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
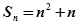 ,那么它的通项公式为an=_________
,那么它的通项公式为an=_________
 ,那么它的通项公式为an=_________
.
,那么它的通项公式为an=_________
. , 则数列的通项an=
, 则数列的通项an=