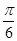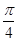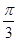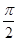题目内容
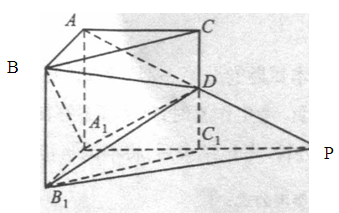
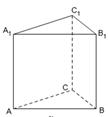
如图,在直三棱柱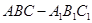 中,
中,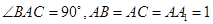 ,
,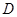 是棱
是棱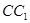 上的一点,
上的一点,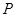 是
是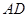 的延长线与
的延长线与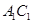 的延长线的交点,且
的延长线的交点,且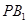 ∥平面
∥平面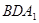 。
。
(1)求证: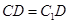 ;
;
(2)求二面角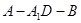 的平面角的余弦值;
的平面角的余弦值;
(3)求点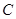 到平面
到平面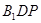 的距离.
的距离.
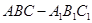 中,
中,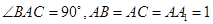 ,
,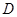 是棱
是棱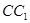 上的一点,
上的一点,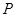 是
是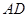 的延长线与
的延长线与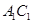 的延长线的交点,且
的延长线的交点,且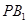 ∥平面
∥平面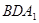 。
。
(1)求证:
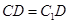 ;
;(2)求二面角
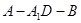 的平面角的余弦值;
的平面角的余弦值;(3)求点
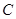 到平面
到平面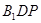 的距离.
的距离.(1)详见解析;(2)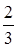 ;(3)
;(3)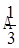
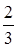 ;(3)
;(3)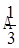
试题分析:(1)连接
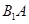 交
交 于
于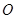 ,由线面平行的性质定理可得
,由线面平行的性质定理可得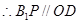 ,,又
,,又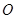 为
为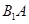 的中点,
的中点,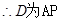 中点。同理可得
中点。同理可得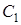 为
为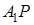 的中点,再根据全等证
的中点,再根据全等证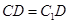 。(2)根据二面角的定义利用垂面法找到二面角,利用三角函数求出即可,详见解析;(3)因为D是
。(2)根据二面角的定义利用垂面法找到二面角,利用三角函数求出即可,详见解析;(3)因为D是 的中点,所以
的中点,所以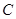 到平面
到平面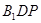 的距离等于
的距离等于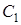 到平面
到平面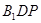 的距离,再根据
的距离,再根据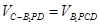 求点到面的距离。
求点到面的距离。试题解析:(1)连接
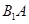 交
交 于
于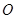 ,
,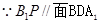 ,
,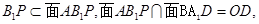
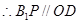 ,又
,又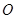 为
为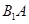 的中点,
的中点,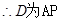 中点,
中点,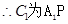 的中点,
的中点,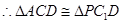
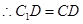 ,D为
,D为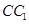 的中点。
的中点。(2)由题意
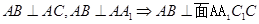 ,过A作
,过A作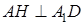 ,连接
,连接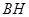 ,则
,则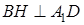 ,
,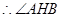 为二面角
为二面角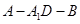 的平面角。在
的平面角。在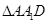 中,
中,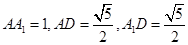 ,
,因为在三角形
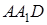 中,
中,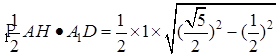 则
则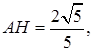
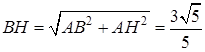 ,所以
,所以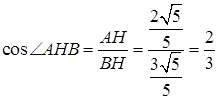
(3)因为
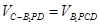 ,所以
,所以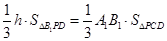 ,
,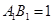
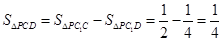 ,
,在
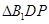 中,
中,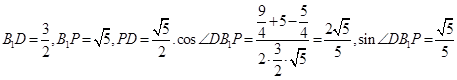 ,
,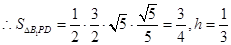

练习册系列答案
相关题目
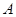 、
、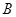 、
、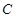 为不在同一直线上的三点,且
为不在同一直线上的三点,且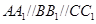 ,
,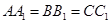 .
.
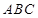 //平面
//平面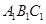 ;
;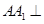 平面
平面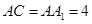 ,
,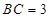 ,
,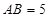 ,求证:
,求证: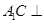 平面
平面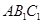 ;
;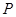 为
为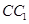 上的动点,求当
上的动点,求当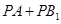 取得最小值时
取得最小值时 的长.
的长.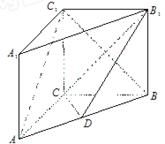
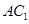 ∥平面
∥平面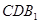 ;
;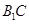 所成角的余弦值.
所成角的余弦值.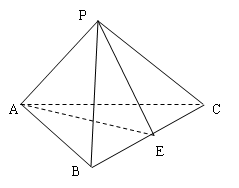
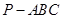 中,
中,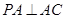 ,
,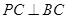 ,
,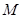 为
为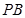 的中点,
的中点,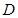 为
为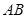 的中点,且
的中点,且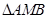 为正三角形.
为正三角形.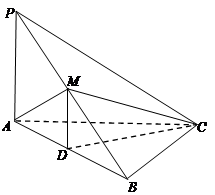
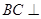 平面
平面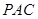 ;
;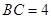 ,
,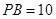 ,求点
,求点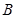 到平面
到平面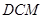 的距离.
的距离.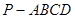 中,底面为直角梯形,
中,底面为直角梯形,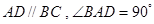 ,
,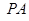 垂直于底面
垂直于底面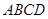 ,
,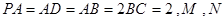 分别为
分别为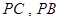 的中点.
的中点.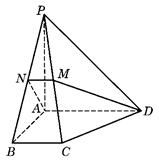
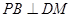 ;
;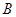 到平面
到平面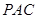 的距离.
的距离.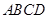 中,
中,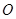 、
、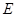 分别是
分别是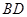 、
、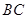 的中点,
的中点,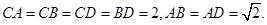
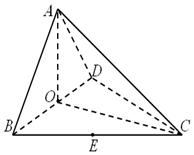
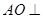 平面
平面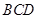 ;
;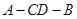 的正切值;
的正切值;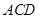 的距离.
的距离. ,那么平面
,那么平面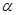 内一定存在直线平行于平面
内一定存在直线平行于平面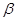 ;
; ,平面
,平面 ,
,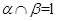 ,那么
,那么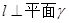 ;
;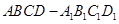 中,
中,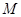 、
、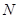 分别是
分别是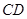 、
、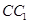 的中点,则异面直线
的中点,则异面直线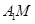 与
与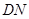 所成角的大小是( )
所成角的大小是( )