题目内容
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
,![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程
的极坐标方程![]() .
.
(1)若曲线![]() 与
与![]() 只有一个公共点,求
只有一个公共点,求![]() 的值;
的值;
(2)![]() 为曲线
为曲线![]() 上的两点,且
上的两点,且![]() ,求
,求![]() 的面积最大值.
的面积最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题(1)将曲线![]() 的参数方程和直线
的参数方程和直线![]() 的极坐标方程化为普通方程,然后利用圆心到直线的距离为半径建立等量关系,求解参数
的极坐标方程化为普通方程,然后利用圆心到直线的距离为半径建立等量关系,求解参数![]() 的值;(2)借助极坐标方程中极角的几何意义和三角变换,将
的值;(2)借助极坐标方程中极角的几何意义和三角变换,将![]() 的面积公式转化为含有一个角的一个三角函数,利用三角函数的图象探求最值问题.
的面积公式转化为含有一个角的一个三角函数,利用三角函数的图象探求最值问题.
(Ⅰ)曲线![]() 是以
是以![]() 为圆心,以
为圆心,以![]() 为半径的圆;
为半径的圆;
直线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
由直线![]() 与圆
与圆![]() 只有一个公共点,则可得
只有一个公共点,则可得![]() ,
,
解得: ![]() (舍),
(舍),![]() .
.
所以:![]()
(Ⅱ)曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
设![]() 的极角为
的极角为![]() ,
, ![]() 的极角为
的极角为![]() ,
,
则![]() ,
,
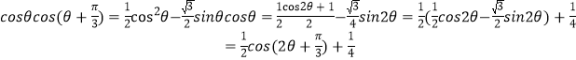 所以当
所以当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
![]() 的面积最大值
的面积最大值![]() .
.
解法二:因为曲线![]() 是以
是以![]() 为圆心,以
为圆心,以![]() 为半径的圆,且
为半径的圆,且![]()
由正弦定理得:![]() ,所以
,所以![]() .
.
由余弦定理得![]() ,
,
所以![]() ,
,
所以![]() 的面积最大值
的面积最大值![]() .
.

练习册系列答案
相关题目