题目内容
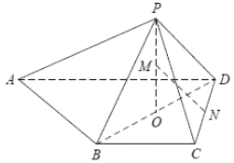
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() 是等边三角形,
是等边三角形,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)证明见解析(Ⅱ)![]()
【解析】
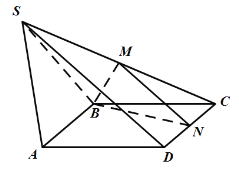
连接![]() ,由已知得,
,由已知得,![]() ,又
,又![]() 是
是![]() 的中点,所以
的中点,所以![]() ,计算可得
,计算可得![]() ,由
,由![]() ,可得
,可得![]() ,可得
,可得![]() 平面
平面![]() ;
;
(Ⅱ)取AB的中点O,连结OS,OD,可得OD∥BN, 由CD⊥OD,CD⊥SD,![]() ,可得
,可得![]() ,
,![]() , OP⊥面SCD, 计算可得OP的值,由
, OP⊥面SCD, 计算可得OP的值,由![]() 可得AB//面SCD, 可得直线
可得AB//面SCD, 可得直线![]() 所成角的正弦值.
所成角的正弦值.
解:(Ⅰ)连接![]() ,由已知得,
,由已知得,![]() ,又
,又![]() 是
是![]() 的中点,所以
的中点,所以![]() .
.
再由![]()
![]() ,所以
,所以![]() ,由
,由![]() ,∴
,∴![]() ,
,![]() ,故
,故![]() .
.
(Ⅱ)取AB的中点O,连结OS,OD,由已知OD= OS=![]() ,OD∥BN
,OD∥BN
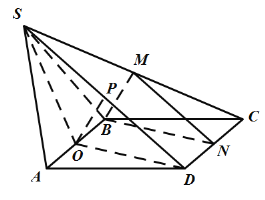
根据(1)有CD⊥OD,CD⊥SD,![]()
所以![]() .又
.又![]()
![]()
![]() 作OP⊥SD,则OP⊥面SCD
作OP⊥SD,则OP⊥面SCD
△SOD中,OD=OS=![]() ,SD=3,
,SD=3,
![]()
∵![]() ,∴AB//面SCD,
,∴AB//面SCD,
![]() 点A到平面SCD的距离等于点O到平面SCD的距离
点A到平面SCD的距离等于点O到平面SCD的距离
设直线![]() 所成角为
所成角为![]() ,
,
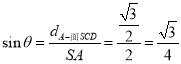 .
.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目