题目内容
(本题16分)设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ;数列
;数列![]() 为等差数列,且
为等差数列,且![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;(2)若
的通项公式;(2)若![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和.
项和.
求证:![]() .
.
解:(1)由![]() ,令
,令![]() ,则
,则![]() ,又
,又![]() ,所以
,所以![]() .
.
![]() ,则
,则![]() . …………………………………………………………………………………….
. …………………………………………………………………………………….
当![]() 时,由
时,由![]() ,可得
,可得![]() . 即
. 即![]() ..
..
所以![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列,于是
为公比的等比数列,于是![]() .
.
(2)数列![]() 为等差数列,公差
为等差数列,公差![]() ,可得
,可得![]() . …
. …
从而![]() . ……………………………………………..
. ……………………………………………..
∴![]()
![]() ………
………

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
(本题满分16分)
设数列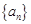 的前
的前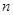 项和为
项和为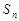 ,若对任意
,若对任意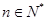 ,都有
,都有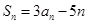 .
.
⑴求数列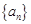 的首项;
的首项;
⑵求证:数列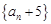 是等比数列,并求数列
是等比数列,并求数列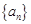 的通项公式;
的通项公式;
⑶数列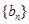 满足
满足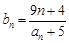 ,问是否存在
,问是否存在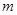 ,使得
,使得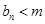 恒成立?如果存在,求出
恒成立?如果存在,求出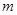 的值,如果不存在,说明理由.
的值,如果不存在,说明理由.
 满足
满足 ,令
,令 .
. 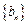 是否为等差数列?并说明理由;
是否为等差数列?并说明理由; ,求
,求 前
前 项的和
项的和 ;
; 使得
使得 三数成等比数列?
三数成等比数列? 满足
满足 ,令
,令 .
.  是否为等差数列?并说明理由;
是否为等差数列?并说明理由; ,求
,求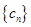 前
前 项的和
项的和 ;
; 使得
使得 三数成等比数列?
三数成等比数列?