题目内容

（1-x）⁴（1+x）⁴的展开式x²的系数是（　　）

A、-4

B、-6

C、6

D、4

分析：先利用平方差进行运算，注意两个展开式的结合分析，把两个因式的积写成一个二项式形式，写出二项式的展开式，求出自变量的指数是2时的系数．

解答：解：∵（1-x）⁴（1+x）⁴=（1-x²）⁴⁴∴二项式的展开式是C₄^r（-x²）^r
∵要求展开式x²的系数，
∴当r=1时，展开式为-4x²，
即展开式的系数是-4，
故选A．

点评：本题重点考查二项展开式中指定项的系数，以及组合思想，重在找寻这些项的来源，若所给的是多于一项的式子，注意做到不要漏项．

练习册系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

本题有（1）、（2）、（3）三个选答题，请考生任选2题作答．
（1）选修4-2：矩阵与变换
已知a，b∈R，若M=

-1	a
b	3

所对应的变换T_M把直线L：2x-y=3变换为自身，求实数a，b，并求M的逆矩阵．
（2）选修4-4：坐标系与参数方程
已知直线l的参数方程：

（t为参数）和圆C的极坐标方程：ρ=2

)．
①将直线l的参数方程化为普通方程，圆C的极坐标方程化为直角坐标方程；
②判断直线l和圆C的位置关系．
（3）选修4-5：不等式选讲
已知函数f（x）=|x-1|+|x-2|．若不等式|a+b|+|a-b|≥|a|f（x）（a≠0，a，b∈R）恒成立，求实数x的范围．

今有一组实验数据如下：

x	0	1	2	3	4
y	1	5	3	1	2

最能近似地表达这些数据规律的函数模型是（　　）

B．y=bx²+ax+1

C．y=x（x-a）²+b

D．y=Asin（ωx+φ）+B

（2006•广州模拟）已知集合A={x|x＞3或x＜-1}，B={x|2＜x＜4}，则A∩B=（　　）

A．{x|-1＜x＜2}

B．{x|2＜x＜4}

C．{x|3＜x＜4}

D．{x|-1＜x＜3}

对于函数f（x），g（x），h（x），如果存在实数a，b，使得h（x）=af（x）+bg（x），那么称h（x）为f（x），g（x）的线性生成函数．
（1）给出如下两组函数，试判断h（x）是否分别为f（x），g（x）的线性生成函数，并说明理由．
第一组： $数学公式$ ；
第二组：f（x）=x²-x，g（x）=x²+x+1，h（x）=x²-x+1．
（2）已知f（x）=log₂x，g（x）=log_0.5x的线性生成函数为h（x），其中a=2，b=1．若不等式3h²（x）+2h（x）+t＜0在x∈[2，4]上有解，求实数t的取值范围；
（3）已知 $数学公式$ 的线性生成函数h（x），其中a＞0，b＞0．若h（x）≥b对a∈[1，2]恒成立，求实数b的取值范围．

对于函数f（x），g（x），h（x），如果存在实数a，b，使得h（x）=af（x）+bg（x），那么称h（x）为f（x），g（x）的线性生成函数．
（1）给出如下两组函数，试判断h（x）是否分别为f（x），g（x）的线性生成函数，并说明理由．
第一组：

；
第二组：f（x）=x²-x，g（x）=x²+x+1，h（x）=x²-x+1．
（2）已知f（x）=log₂x，g（x）=log_0.5x的线性生成函数为h（x），其中a=2，b=1．若不等式3h²（x）+2h（x）+t＜0在x∈[2，4]上有解，求实数t的取值范围；
（3）已知

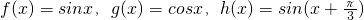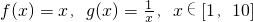的线性生成函数h（x），其中a＞0，b＞0．若h（x）≥b对a∈[1，2]恒成立，求实数b的取值范围．