题目内容
设函数 ,
, 图象的一条对称轴是直线
图象的一条对称轴是直线 .
.
(1)求 ;
;
(2)求函数 的单调增区间;
的单调增区间;
(3)画出函数 在区间[0,π]上的图象.
在区间[0,π]上的图象.
(1) ;(2)
;(2) ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)由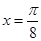 是函数
是函数 图象的对称轴及函数
图象的对称轴及函数 的对称轴为
的对称轴为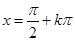 ,
,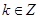 可知
可知 ,
, ,
,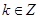 ,再根据
,再根据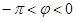 ,则
,则 ,从而
,从而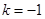 ,
, ;(2)由(1)及
;(2)由(1)及 的递增区间为
的递增区间为 ,
,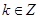 ,可知令
,可知令 ,解得
,解得 ,
,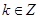 ,从而函数
,从而函数 的单调增区间为
的单调增区间为 ,
,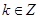 ;(3)通过列表将
;(3)通过列表将 图象上的几个特征点(端点,最值点,与
图象上的几个特征点(端点,最值点,与 轴交点)列出,描点,用光滑曲线连接,即可得到
轴交点)列出,描点,用光滑曲线连接,即可得到 在区间
在区间 上的图象.
上的图象.
试题解析:(1)∵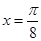 是函数
是函数 图象的对称轴,
图象的对称轴,
∴ ,
, ,
,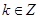 ,又∵
,又∵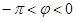 ,∴
,∴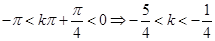 ,
,
∵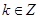 ,∴
,∴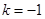 ,∴
,∴ ;
;
(2)由(1)知 ,∴
,∴ ,
,
令 ,解得
,解得 ,
,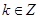 ,
,
∴函数 的单调增区间为
的单调增区间为 ,
,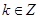 ;
;
(3)由 知:
知:


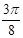





 练习册系列答案
练习册系列答案
暑假作业新世界出版社系列答案
创新成功学习快乐暑假云南科技出版社系列答案
暑假生活安徽教育出版社系列答案
假期生活智趣暑假系列答案
假期园地复习计划系列答案
学苑新报暑假专刊系列答案
暑假乐园广东人民出版社系列答案
全能测控期末大盘点系列答案
快乐暑假江苏教育出版社系列答案
 相关题目
相关题目
 .
. ;
; 是第三象限角,且
是第三象限角,且 ,求
,求 的图像关于直线
的图像关于直线 对称,且图像上相邻两个最高点的距离为
对称,且图像上相邻两个最高点的距离为 .
. 和
和 的值;
的值; ,求
,求 的值.
的值.
 ,
,
 ,且
,且 的图象的一个对称中心到最近的对称轴的距离为
的图象的一个对称中心到最近的对称轴的距离为 ,(1)求
,(1)求 的值;(2)求
的值;(2)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
 的周期和单调递增区间;
的周期和单调递增区间; 在
在 上有解,求实数m的取值范围.
上有解,求实数m的取值范围. 和
和 为方程
为方程 的两根,求
的两根,求 ;(2)
;(2) 的值。
的值。 ,
, ,且
,且 .
. 的值;
的值; ,
, ,求
,求 .
. 的图象向右平移
的图象向右平移 个单位后,图象关于直线
个单位后,图象关于直线 对称, 则m最小值为 .
对称, 则m最小值为 .