题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求
,求![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)讨论![]() 的单调性.
的单调性.
【答案】![]()
![]() ;
;![]() 当
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增;
上单调递增;
当![]() 时, 函数
时, 函数![]() 在区间
在区间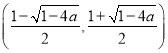 上单调递减;
上单调递减;
在区间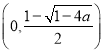 ,
,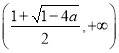 上单调递增.
上单调递增.
【解析】
![]() 根据题意,求出函数
根据题意,求出函数![]() 的导数
的导数![]() ,由导数的几何意义知函数
,由导数的几何意义知函数![]() 在
在![]() 处切线的斜率
处切线的斜率![]() ,代入点斜式方程即可求解;
,代入点斜式方程即可求解;
![]() 根据题意,求出函数
根据题意,求出函数![]() 的导数
的导数![]() ,分
,分![]() 和
和![]() 两种情况,求出
两种情况,求出![]() 所对的
所对的![]() 的取值范围,据此可以判断函数
的取值范围,据此可以判断函数![]() 的单调性.
的单调性.
![]() 当
当![]() 时,
时,![]() ,则
,则![]() ,
,
所以![]() ,由导数的几何意义可知,
,由导数的几何意义可知,
函数![]() 在
在![]() 处切线的斜率
处切线的斜率![]() ,
,
所以函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
即函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ;
;
![]() 因为函数
因为函数![]() ,
,
所以![]() ,即
,即![]() ,
,
当![]() 时,
时, ![]() ,因为
,因为![]() ,
,
所以![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上单调递增;
上单调递增;
当![]() 时,因为方程
时,因为方程![]() 的两根为
的两根为![]() ,
,
所以由![]() ,解得
,解得![]() 或
或![]() ,
,
由![]() ,解得
,解得![]() ,
,
所以函数![]() 在区间
在区间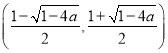 上单调递减;
上单调递减;
在区间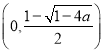 ,
,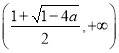 上单调递增.
上单调递增.
综上可知, 当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增;
上单调递增;
当![]() 时, 函数
时, 函数![]() 在区间
在区间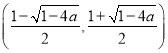 上单调递减;
上单调递减;
在区间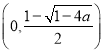 ,
,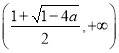 上单调递增.
上单调递增.

练习册系列答案
相关题目
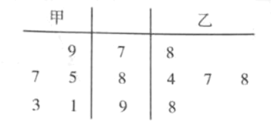
【题目】某美术学院2018年在山西招生,报名人数很多.工作人员在某个市区抽取了该区2018年美术招生考试成绩中200名学生的色彩和素描的初试成绩,按成绩分组,得到的频率分布表如下图所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 24 | 0.12 |
第2组 |
| ① | 0.18 |
第3组 |
| 64 | 0.32 |
第4组 |
| 60 | ② |
第5组 |
| 16 | 0.08 |
合计 | 200 | 1.00 | |
(1)请先求出频率分布表中①、②位置相应数据,再在答题纸上完成下列频率分布直方图,并由频率分布直方图估算中位数;
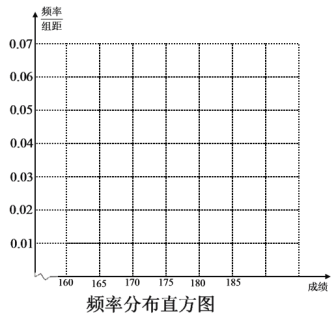
(2)为了能更清楚地了解该市学生的情况,该美院决定在复试以前先进行抽样调研.但受场地和教授人数的客观限制,决定从第3组选出3人,第4组选出2人,第5组选出1人,然后从这6人中再选出2人进行调研,求这2人均来自第三组的概率.