题目内容
当a为何值时,直线l1:(a+2)x+(1-a)y-1=0与直线l2:(a-1)x+(2a+3)y+2=0互相垂直?
思路分析一:分类讨论,利用直线垂直的充要条件进行求解.
解:由题意,直线l1⊥l2.
(1)若1-a=0,即a=1,
此时l1:3x-1=0,直线l2:5y+2=0,显见l1与l2垂直.
(2)若2a+3=0,即a=-![]() 时,
时,
直线l1:x+5y-2=0与直线l2:5x-4=0不?垂直.
(3)若1-a≠0,且2a+3≠0,则直线l1、l2的斜率k1、k2存在.
k1=-![]() ,k2=-
,k2=-![]() .
.
当l1⊥l2时,k1·k2=-1,
即(-![]() )·(-
)·(-![]() )=-1.∴a=-1.
)=-1.∴a=-1.
综上,可知当a=1或a=-1时,直线l1⊥l2.
思路分析二:利用结论“直线l1和l2的方程分别是l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,则直线l1⊥l2的充要条件是A1A2+B1B2=0”解题.
解:由于直线l1⊥l2,
所以(a+2)(a-1)+(1-a)(2a+3)=0.
解得a=±1.
故a=1或a=-1时,直线l1⊥l2.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 的最值.
的最值.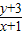 的最值.
的最值.