题目内容
(1)一扇形的圆心角为72°,半径等于20cm,求扇形的弧长和面积;
(2)已知sin(π+θ)=
,求
+
的值.
(2)已知sin(π+θ)=
| 4 |
| 5 |
| cos(π+θ) |
| cosθ[cos(π-θ)-1] |
| cos(θ-2π) |
| cosθcos(π-θ)+cos(θ-2π) |
分析:(1)设这个扇形的弧长为l,面积为S,将72°化为弧度,利用弧长公式与扇形的面积公式即可求扇形的弧长和面积;
(2)利用诱导公式求得sinθ,再对所求式化简求值即可.
(2)利用诱导公式求得sinθ,再对所求式化简求值即可.
解答:解:(1)设这个扇形的弧长为l,面积为S,因为72°=
…(2分)
∴该扇形的弧长l=
×20=8π(cm)…(4分),
扇形的面积S=
×8π×20=80π(cm2)…(6分)
(2 )由sin(π+θ)=
得:sinθ=-
…(8分)
∴原式=
+
=
+
=
…(10分)
=
=
.…(12分)
| 2π |
| 5 |
∴该扇形的弧长l=
| 2π |
| 5 |
扇形的面积S=
| 1 |
| 2 |
(2 )由sin(π+θ)=
| 4 |
| 5 |
| 4 |
| 5 |
∴原式=
| -cosθ |
| cosθ(-cosθ-1) |
| cosθ |
| cosθ(-cosθ)+cosθ |
=
| 1 |
| 1+cosθ |
| 1 |
| 1-cosθ |
=
| 2 |
| 1-cos2θ |
=
| 2 | ||
(-
|
| 25 |
| 8 |
点评:本题考查扇形的弧长公式与面积公式,考查利用诱导公式化简求值,考查运算能力,属于中档题.

练习册系列答案
相关题目
 ,求
,求 的值.
的值.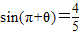 ,求
,求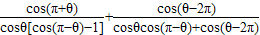 的值.
的值.