题目内容
已知a为实数,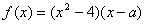 .
.
(1) 求导数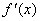 ;
;
(2) 若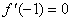 ,求
,求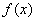 在[-2,2] 上的最大值和最小值;
在[-2,2] 上的最大值和最小值;
(3) 若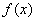 在(-∞,-2]和[2,+∞)上都是递增的,求a的取值范围。
在(-∞,-2]和[2,+∞)上都是递增的,求a的取值范围。
解:(1)由原式得
∴
(2)由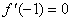 得
得 ,此时有
,此时有 .
.
由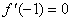 得
得 或x=-1 ,
或x=-1 ,
又
所以f(x)在[-2,2]上的最大值为 最小值为
最小值为
(3)解法一: 的图象为开口向上且过点(0,-4)的抛物线,
的图象为开口向上且过点(0,-4)的抛物线,
由条件得

即 ∴-2≤a≤2. 所以a的取值范围为[-2,2].
∴-2≤a≤2. 所以a的取值范围为[-2,2].
解法二:令 即
即
由求根公式得: 
所以 在
在 和
和 上非负.
上非负.
由题意可知,当x≤-2或x≥2时, 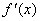 ≥0,
≥0,
从而x1≥-2, x2≤2,
即 解不等式组得-2≤a≤2.
解不等式组得-2≤a≤2.
∴a的取值范围是[-2,2].

练习册系列答案
相关题目
 ,则
,则 在复平面上对应的点位于第 象限
在复平面上对应的点位于第 象限 ;
; 中,
中, ,如果不等式
,如果不等式 恒成立,则实数
恒成立,则实数 的取值范围是( )
的取值范围是( )  B.
B.
 D.
D.
 在
在 上为增函数,则实数
上为增函数,则实数 的取值范围是_________
的取值范围是_________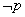 ”与命题“
”与命题“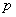 或
或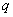 ”都是真命题,那么命题
”都是真命题,那么命题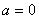 ,则
,则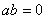 ”的否命题是:“若
”的否命题是:“若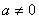 ,则
,则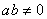 ”
”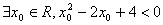 ,则
,则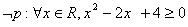
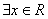 ,使
,使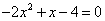 ”是真命题.
”是真命题. ,
, ,
, ,点Q在直线OP上运动,则当
,点Q在直线OP上运动,则当 取得最小值时,点Q的坐标为( ).
取得最小值时,点Q的坐标为( ). B.
B. C.
C.  D.
D.
 (a,b∈R),其中i为虚数单位,则a+b=( )
(a,b∈R),其中i为虚数单位,则a+b=( ) B.1 C.2 D.3
B.1 C.2 D.3