题目内容
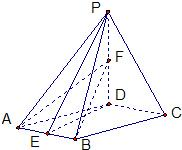已知四棱锥P-ABCD，底面ABCD是菱形，∠DAB=60°，PD⊥平面ABCD，PD=AD，点E为AB中点，点F为PD中点．（1）证明平面PED⊥平面PAB；
（2）求二面角P-AB-F的平面角的余弦值．
分析：（1）先由已知条件证明∴△ADB为等边三角形，AB⊥DE，易证AB⊥PD，得到AB⊥面PED，进而证明面PED⊥面PAB．
（2）先由二面角的定义找出二面角的平面角，把二面角的平面角放在一个三角形中，求出此角的余弦值．
（2）先由二面角的定义找出二面角的平面角，把二面角的平面角放在一个三角形中，求出此角的余弦值．
解答：
（1）证明：连接BD．∵AB=AD，∠DAB=60°，∴△ADB为等边三角形．
∵E是AB中点，∴AB⊥DE．（2分）∵PD⊥面ABCD，AB?面ABCD，∴AB⊥PD．
∵DE?面PED，PD?面PED，DE∩PD=D，∴AB⊥面PED． （4分）
∵AB?面PAB，∴面PED⊥面PAB． （6分）
（2）解：∵AB⊥平面PED，PE?面PED，∴AB⊥PE．
连接EF，∵EF?PED，∴AB⊥EF．∴∠PEF为二面角P-AB-F的平面角．（9分）
设AD=2，那么PF=FD=1，DE=
．
在△PEF中，PE=
，EF=2，PF=1，
∴cos∠PEF=
=
，
即二面角P-AB-F的平面角的余弦值为
.（12分）
（1）证明：连接BD．∵AB=AD，∠DAB=60°，∴△ADB为等边三角形．∵E是AB中点，∴AB⊥DE．（2分）∵PD⊥面ABCD，AB?面ABCD，∴AB⊥PD．
∵DE?面PED，PD?面PED，DE∩PD=D，∴AB⊥面PED． （4分）
∵AB?面PAB，∴面PED⊥面PAB． （6分）
（2）解：∵AB⊥平面PED，PE?面PED，∴AB⊥PE．
连接EF，∵EF?PED，∴AB⊥EF．∴∠PEF为二面角P-AB-F的平面角．（9分）
设AD=2，那么PF=FD=1，DE=
| 3 |
在△PEF中，PE=
| 7 |
∴cos∠PEF=
(
| ||
2×2
|
5
| ||
| 14 |
即二面角P-AB-F的平面角的余弦值为
5
| ||
| 14 |
点评：本小题主要考查空间中的线面关系，四棱锥的有关概念及余弦定理等基础知识，考查空间想象能力和推理能力．
练习册系列答案
相关题目
如图，已知四棱锥P--ABC的底面ABCD为正方形，PA⊥平面ABCD，PA=AB=2，e为PC的中点，F为AD的中点．
如图，已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，AB=BC=2CD=2，PB=PC，侧面PBC⊥底面ABCD，O是BC的中点．
已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，E为BC中点，AE与BD交于O点，AB=BC=2CD=2，BD⊥PE．
如图，已知四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是直角梯形，∠DAB=∠ABC=90°，E是线段PC上一点，PC⊥平面BDE．