Question

已知三棱柱ABC—A₁B₁C₁，在某个空间直解坐标系中，=(,-,0),=(m,0,0),=(0,0,n),其中m、n＞0.

（1）证明三棱柱ABC—A₁B₁C₁是正三棱柱；

（2）若m=n,求直线CA₁与平面A₁ABB₁所成解的大小.

Answer 1

（1）证明：=-

=(m,0,0)-(,-,0)

=(,,0),

||=||=||=m,

∴△ABC为正三角形.

    又·=0，·=0，

∴AA₁⊥AB,AA₁⊥AC.

    又AB∩AC=A,∴AA₁⊥平面ABC.

∴三棱术ABC—A₁B₁C₁是正三棱柱.

（2）解：作CD⊥AB于D，连结A₁D.

∵AA₁⊥平面ABC，∴面AA₁B₁B⊥平面ABC.

∴CD⊥平面AA₁B₁B.

    因此A₁D为斜线A₁C在平面AA₁B₁B上的射影.

∠CA₁D为直线CA₁与平面AA₁B₁B所成的角.

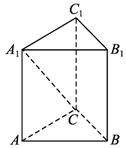
    在Rt△CDA₁中，CD=m,

A₁D==.

tan∠CA₁D===.

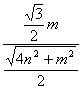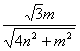    又m=n,

∴tan∠CA₁D=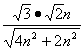=1.

    又0＜∠CA₁D＜,

∴∠CA₁D=45°.