题目内容
15.利用单位圆写出符合下列条件的角x的范围.(1)sinx<-$\frac{\sqrt{2}}{2}$;
(2)|cosx|≤$\frac{1}{2}$;
(3)sinx≥-cosx.
分析 由已知条件作出单位圆,利用单位圆求出在[0,2π)内满足条件的x有范围,再利用终边相同的角的概念,能求出符合条件的角x的范围.
解答 解:(1)∵sinx<-$\frac{\sqrt{2}}{2}$,
∴作出单位图,如下图:
结合单位圆,得$\frac{5π}{4}<x<\frac{7π}{4}$,
∴符合sinx<-$\frac{\sqrt{2}}{2}$的角x的范围为{x|$\frac{5π}{4}+2kπ<x<\frac{7π}{4}+2kπ$,k∈Z}.
(2)∵|cosx|≤$\frac{1}{2}$,即-$\frac{1}{2}≤cosx≤\frac{1}{2}$,
∴作出单位图,如下图: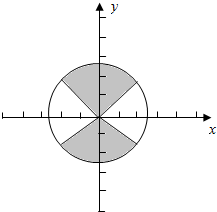
结合单位圆,得$\frac{π}{3}≤α≤\frac{2π}{3}$或$\frac{4π}{3}≤α≤\frac{5π}{3}$,
∴符合|cosx|≤$\frac{1}{2}$的角x的范围为{x|$kπ+\frac{π}{3}≤α≤kπ+\frac{2π}{3}$,k∈Z}.
(3)∵sinx≥-cosx,
∴作出单位图,如下图: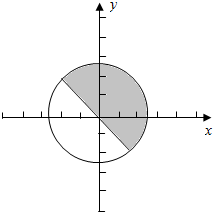
结合单位圆,得0≤x≤$\frac{3π}{4}$或$\frac{7π}{4}$≤x<2π,
∴符合sinx≥-cosx的角x的范围为{x|$2kπ≤x≤\frac{3π}{4}+2kπ$,或$\frac{7π}{4}+2kπ≤x<2kπ+2π$,k∈Z}.
点评 本题考查满足条件的角的取值范围的求法,是基础题,解题时要认真审题,注意单位圆的性质的合理运用.

练习册系列答案
相关题目
6.已知等差数列{an}的前n项和为Sn,a23+a2=2014,则a20133+a2013=-2014,则S2014=( )
| A. | 2014 | B. | 1 | C. | 0 | D. | -1 |
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,AD⊥AB,BC∥AD,AD=2AB=2BC=2.求证:PC⊥CD.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,AD⊥AB,BC∥AD,AD=2AB=2BC=2.求证:PC⊥CD.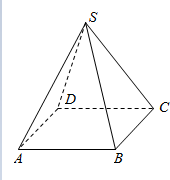 如图,在正四棱锥S-ABCD中,底面边长为6cm,侧棱长为3$\sqrt{5}$cm.
如图,在正四棱锥S-ABCD中,底面边长为6cm,侧棱长为3$\sqrt{5}$cm.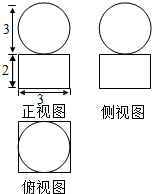 设如图是某几何体的三视图,求该几何体的体积和表面积.
设如图是某几何体的三视图,求该几何体的体积和表面积.