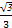题目内容
已知椭圆C: +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 .双曲线x2-y2=1的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )
.双曲线x2-y2=1的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )
 +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 .双曲线x2-y2=1的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )
.双曲线x2-y2=1的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )A. + +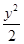 =1 =1 | B. + + =1 =1 |
C.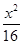 + + =1 =1 | D. + + =1 =1 |
D
利用椭圆离心率的概念和双曲线渐近线求法求解.
∵椭圆的离心率为 ,
,
∴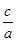 =
=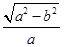 =
= ,
,
∴a=2b.
∴椭圆方程为x2+4y2=4b2.
∵双曲线x2-y2=1的渐近线方程为x±y=0,
∴渐近线x±y=0与椭圆x2+4y2=4b2在第一象限的交点为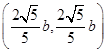 ,
,
∴由圆锥曲线的对称性得四边形在第一象限部分的面积为
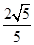 b×
b×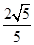 b=4,
b=4,
∴b2=5,
∴a2=4b2=20.
∴椭圆C的方程为 +
+ =1.
=1.
故选D.
∵椭圆的离心率为
 ,
,∴
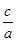 =
=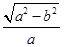 =
= ,
,∴a=2b.
∴椭圆方程为x2+4y2=4b2.
∵双曲线x2-y2=1的渐近线方程为x±y=0,
∴渐近线x±y=0与椭圆x2+4y2=4b2在第一象限的交点为
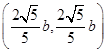 ,
,∴由圆锥曲线的对称性得四边形在第一象限部分的面积为
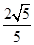 b×
b×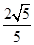 b=4,
b=4,∴b2=5,
∴a2=4b2=20.
∴椭圆C的方程为
 +
+ =1.
=1.故选D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的离心率为
的离心率为 ,短轴长是2.
,短轴长是2.
 时,求k的取值范围.
时,求k的取值范围. +
+ =1(a>b>0)的焦距等于2|ON|,且过点(
=1(a>b>0)的焦距等于2|ON|,且过点( ,
, ).
).
 ,左、右准线分别为l1:x=-m-1,l2:x=m+1,且l1、l2分别与直线y=x相交于A、B两点.
,左、右准线分别为l1:x=-m-1,l2:x=m+1,且l1、l2分别与直线y=x相交于A、B两点. ,求椭圆的方程;
,求椭圆的方程; ·
· <7时,求椭圆离心率的取值范围.
<7时,求椭圆离心率的取值范围.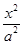 +
+ =1(a>b>0),抛物线C2:x2+by=b2.
=1(a>b>0),抛物线C2:x2+by=b2.
 ,
, b),又M,N为C1与C2不在y轴上的两个交点,若△AMN的垂心为B(0,
b),又M,N为C1与C2不在y轴上的两个交点,若△AMN的垂心为B(0, b),且△QMN的重心在C2上,求椭圆C1和抛物线C2的方程.
b),且△QMN的重心在C2上,求椭圆C1和抛物线C2的方程. +
+ =1的交点在x轴上的射影恰好是椭圆的焦点,则椭圆C的离心率为( )
=1的交点在x轴上的射影恰好是椭圆的焦点,则椭圆C的离心率为( )



 +
+ =1(a>b>0)的左,右焦点分别为F1,F2,点P(a,b)满足|PF2|=|F1F2|.
=1(a>b>0)的左,右焦点分别为F1,F2,点P(a,b)满足|PF2|=|F1F2|. )2=16相交于M,N两点,且|MN|=
)2=16相交于M,N两点,且|MN|= |AB|,求椭圆的方程.
|AB|,求椭圆的方程. 的焦点
的焦点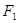 、
、 ,点
,点 为其上的动点,当∠
为其上的动点,当∠