题目内容
已知函数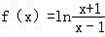
（1）求函数f（x）的定义域，并判断函数f（x）的奇偶性；
（2）对于x∈[2，6]，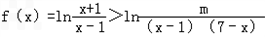
恒成立，
求实数m取值范围．
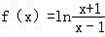
（1）求函数f（x）的定义域，并判断函数f（x）的奇偶性；
（2）对于x∈[2，6]，
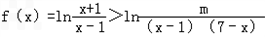恒成立，求实数m取值范围．
解：（1）由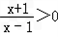
，解得x＜﹣1或x＞1，
∴定义域为（﹣∞，﹣1）∪（1，+∞）
当x∈（﹣∞，﹣1）∪（1，+∞）时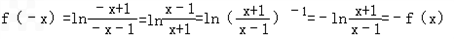
∴
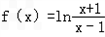是奇函数．
（2）由x∈[2，6]时，
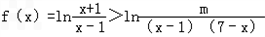恒成立，
∴
，
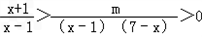∵x∈[2，6]，
∴0＜m＜（x+1）（7﹣x）在x∈[2，6]成立
令g（x）=（x+1）（7﹣x）=﹣（x﹣3）2+16，
x∈[2，6]， 由二次函数的性质可知x∈[2，3]时函数单调递增，
x∈[3，6]时函数单调递减，
∴x∈[2，6]时，g（x）min=g（6）=7
∴0＜m＜7
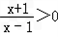，解得x＜﹣1或x＞1，∴定义域为（﹣∞，﹣1）∪（1，+∞）
当x∈（﹣∞，﹣1）∪（1，+∞）时
∴
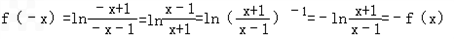
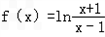是奇函数． （2）由x∈[2，6]时，
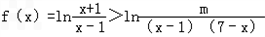恒成立，∴
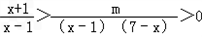， ∵x∈[2，6]，
∴0＜m＜（x+1）（7﹣x）在x∈[2，6]成立
令g（x）=（x+1）（7﹣x）=﹣（x﹣3）2+16，
x∈[2，6]， 由二次函数的性质可知x∈[2，3]时函数单调递增，
x∈[3，6]时函数单调递减，
∴x∈[2，6]时，g（x）min=g（6）=7
∴0＜m＜7
练习册系列答案
应用题作业本系列答案
相关题目
（1）求函数
在区间[1，
]上的最大值、最小值；
）上，函数
图象的下方；
，求证：
≥
。（
）
的极值点；
过点（0，—1），并且与曲线
相切，求直线
，其中
，求函数
在
上的最小值.（其中e为自然对数的底数）