题目内容
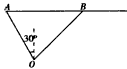
某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上.在小艇出发时,轮船位于港口O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇,
(Ⅰ)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少??
(Ⅱ)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向和航行速度的大
小),使得小艇能以最短时间与轮船相遇,并说明理由。
(Ⅰ)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少??
(Ⅱ)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向和航行速度的大
小),使得小艇能以最短时间与轮船相遇,并说明理由。
解:(Ⅰ)设相遇时小艇航行的距离为S海里,则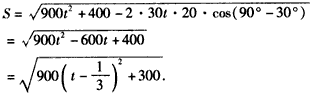 故当 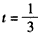 时, 时,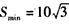 ,此时 ,此时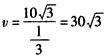 , ,即,小艇以 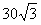 海里/小时的速度航行,相遇时小艇的航行距离最小. 海里/小时的速度航行,相遇时小艇的航行距离最小. |
|
| (Ⅱ)设小艇与轮船在B处相遇,则v2t2=400+900t2-2·20·30t·cos(90°-30°), 故 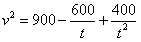 , ,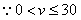 , ,∴ 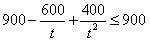 , ,即 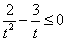 ,解得 ,解得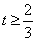 , ,又 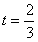 时,v=30, 时,v=30,故v=30时,t取得最小值,且最小值等于 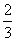 , ,此时,在△OAB中,有OA=OB=AB=20,故可设计航行方案如下: 航行方向为北偏东30°,航行速度为30海里/小时,小艇能以最短时间与轮船相遇. |
 |

练习册系列答案
相关题目

 处,并正以30海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以
处,并正以30海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以 海里/小时的航行速度匀速行驶,经过
海里/小时的航行速度匀速行驶,经过 小时与轮船相遇。
小时与轮船相遇。