题目内容
设z∈C，且（1+2i）
=4+3i（i为虚数单位），则z=
．
. |
| z |
2+i
2+i
，|z|=| 5 |
| 5 |
分析：由题意可得
=
，利用两个复数代数形式的除法法则化简为2-i，由共轭复数的定义求出z，从而求出|z|．
. |
| z |
| 4+3i |
| 1+2i |
解答：解：∵（1+2i）
=4+3i，∴
=
=
=
=2-i，
∴z=2+i，|z|=
．
故答案为 2+i，
. |
| z |
. |
| z |
| 4+3i |
| 1+2i |
| (4+3i)(1-2i) |
| (1+2i)(1-2i) |
| 10-5i |
| 5 |
∴z=2+i，|z|=
| 5 |
故答案为 2+i，
| 5 |
点评：本题主要考查两个复数代数形式的除法，共轭复数的定义，属于基础题．
练习册系列答案
相关题目
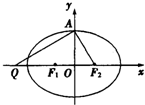（2012•河南模拟）设椭圆
|＝2＋i，则z＝
±
)＋i
＋i
|=2+i，则z=
±
）+i
+i