Question

如图2-1-6,在△ABC中,AD⊥BC于D,DF⊥AC于F,DE⊥AB于E.

求证:(1)AP·DP=EP·FP;

(2)△AEF∽△ACB.

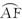
图2-1-6

Answer 1

思路分析：欲证AP·DP=EP·FP,只需证△APE∽△FPD,只需证∠1=∠2.

证明:(1)∵DE⊥AB,DF⊥AC,

∴E、F在以AD为直径的圆上.

∵=,∴∠1=∠2.

∴△APE∽△FPD.∴.

∴AP·DP=EP·FP.

(2)∵∠C+∠CAD=90°,∠2+∠CAD=90°,

∴∠2=∠C.

又∵∠1=∠2,∴∠1=∠C.

∴△AEF∽△ACB.