题目内容
已知命题p:方程a2x2+ax-2=0在[-1,1]上有解,命题q:函数f(x)=x2+2ax+2a的值域为[0,+∞),若命题“p或q”是假命题,求实数a的取值范围.
分析:分别求出命题p,q成立的等价条件,利用“p或q”是假命题,求实数a的取值范围.
解答:解:当a=0时,方程等价为-2=0,不成立.
若a≠0,由a2x2+ax-2=0,得(ax+2)(ax-1)=0,即方程的根为x=-
或x=
.
∵方程a2x2+ax-2=0在[-1,1]上有解,
∴|-
|≤1或|
|≤1,解得|a|≥2或|a|≥1,
即|a|≥1,解得a≥1或a≤-1,
即p:a≥1或a≤-1.
若函数f(x)=x2+2ax+2a的值域为[0,+∞),则判别式△=(2a)2-8a=0,
解得a=0或a=2,即q:a=0或a=2,
∴p或q为:a≥1或a≤-1或a=0,
∵“p或q”为假命题时,
∴-1<a<1且a≠0,即a∈(-1,0)∪(0,1).
若a≠0,由a2x2+ax-2=0,得(ax+2)(ax-1)=0,即方程的根为x=-
| 2 |
| a |
| 1 |
| a |
∵方程a2x2+ax-2=0在[-1,1]上有解,
∴|-
| 2 |
| a |
| 1 |
| a |
即|a|≥1,解得a≥1或a≤-1,
即p:a≥1或a≤-1.
若函数f(x)=x2+2ax+2a的值域为[0,+∞),则判别式△=(2a)2-8a=0,
解得a=0或a=2,即q:a=0或a=2,
∴p或q为:a≥1或a≤-1或a=0,
∵“p或q”为假命题时,
∴-1<a<1且a≠0,即a∈(-1,0)∪(0,1).
点评:本题主要考查复合命题与简单命题之间的关系,利用条件先求出p,q成立的等价条件是解决此类问题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
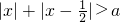 恒成立;若P或q为真,P且q为假,求实数a的取值范围.
恒成立;若P或q为真,P且q为假,求实数a的取值范围. 恒成立;若P或q为真,P且q为假,求实数a的取值范围.
恒成立;若P或q为真,P且q为假,求实数a的取值范围.