题目内容
已知直线l1:3x-y+12=0和l2:3x+2y-6=0,求l1和l2及y轴所围成的三角形面积. 
所围成的三角形面积为9.
解:如图,设l1,l2的交点为A(xa,ya),
如图,设l1,l2的交点为A(xa,ya),解方程组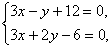
得x=-2,y=6.
∴
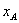=-2.
设直线l1,l2与y轴的交点分别为B(0,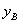
),C(0,
),
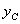求得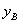="12," 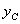=3.
∴|BC|=|
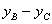|=9.
又A点到y轴距离为|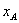|=2,
∴
.
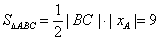∴l1和l2及y轴所围成的三角形面积为9.
如图,设l1,l2的交点为A(xa,ya),解方程组
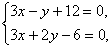得x=-2,y=6.∴
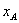=-2.设直线l1,l2与y轴的交点分别为B(0,
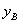),C(0,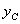),求得
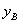="12," 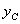=3.∴|BC|=|
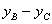|=9.又A点到y轴距离为|
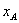|=2,∴
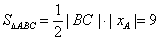.∴l1和l2及y轴所围成的三角形面积为9.
练习册系列答案
相关题目
，
，
，
，试判断直线
与
的位置关系．
与直线2x+3y-6=0的交点位于第一象限，则直线l的倾斜角的取值范围是( ) 
，
，
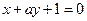构成三角形的条件．