题目内容
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 短轴的两个顶点与右焦点的连线构成等边三角形,两准线之间的距离为
短轴的两个顶点与右焦点的连线构成等边三角形,两准线之间的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
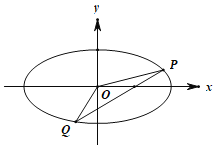
(2)直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,设直线
两点,设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .已知
.已知![]() .
.
①求![]() 的值;
的值;
②当![]() 的面积最大时,求直线
的面积最大时,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() .
.
【解析】
(1)设椭圆的焦距为![]() ,则
,则![]() .利用短轴的两个顶点与右焦点的连线构成等边三角形,求出
.利用短轴的两个顶点与右焦点的连线构成等边三角形,求出![]() ,
,![]() ,然后求解椭圆
,然后求解椭圆![]() 的标准方程.
的标准方程.
(2)①设![]() ,
,![]() ,
,![]() ,
,![]() ,联立
,联立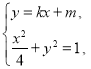 利用韦达定理,通过直线的斜率求解即可;②由①得
利用韦达定理,通过直线的斜率求解即可;②由①得![]() ,直线
,直线![]() 的方程为
的方程为![]() ,然后求解弦长,点到直线的距离,求解三角形的面积,然后求解即可.
,然后求解弦长,点到直线的距离,求解三角形的面积,然后求解即可.
解:(1)设椭圆的焦距为![]() ,则
,则![]() .
.
因为短轴的两个顶点与右焦点的连线构成等边三角形,
所以![]() .
.
又两准线间的距离为![]() ,则
,则![]() ,
,
所以![]() ,
,![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)①设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
联立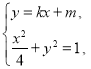 消去
消去![]() 得
得![]() ,
,
![]() ,化简得
,化简得![]() ,
,
所以![]() ,
,![]() ,
,
又![]() 的斜率
的斜率![]() ,
,![]() 的斜率
的斜率![]() ,
,
所以![]() ,
,
化简得![]() ,
,
所以![]() .又因为
.又因为![]() ,即
,即![]() ,
,
又![]() ,所以
,所以![]() .
.
②由①得![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
且![]() ,
,![]() ,
,![]() .
.
又![]() ,所以
,所以![]() .
.
所以![]()
![]() ,
,
点![]() 到直线
到直线![]() 的距离
的距离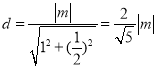 ,
,
所以![]() ,
,
当且仅当![]() ,即
,即![]() 时,
时,![]() 的面积最大,
的面积最大,
所以,直线![]() 的方程为
的方程为![]() .
.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案【题目】过椭圆![]() 的左顶点
的左顶点![]() 作斜率为2的直线,与椭圆的另一个交点为
作斜率为2的直线,与椭圆的另一个交点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,已知
,已知![]() .
.
(1)求椭圆的离心率;
(2)设动直线![]() 与椭圆有且只有一个公共点
与椭圆有且只有一个公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() ,若
,若![]() 轴上存在一定点
轴上存在一定点![]() ,使得
,使得![]() ,求椭圆的方程.
,求椭圆的方程.
【题目】稠环芳香烃化合物中有不少是致癌物质,比如学生钟爱的快餐油炸食品中会产生苯并芘,它是由一个苯环和一个芘分子结合而成的稠环芳香烃类化合物,长期食用会致癌.下面是一组稠环芳香烃的结构简式和分子式:
名称 | 萘 | 蒽 | 并四苯 | … | 并n苯 |
结构简式 |
|
|
| … | … |
分子式 |
|
|
| … | … |
由此推断并十苯的分子式为________.
【题目】噪声污染已经成为影响人们身体健康和生活质量的严重问题,为了了解声音强度![]() (单位:分贝)与声音能量(单位:
(单位:分贝)与声音能量(单位:![]() )之间的关系,将测量得到的声音强度
)之间的关系,将测量得到的声音强度![]() 和声音能量
和声音能量![]() (
(![]() =1,2…,10)数据作了初步处理,得到如图散点图及一些统计量的值.
=1,2…,10)数据作了初步处理,得到如图散点图及一些统计量的值.

|
|
|
|
|
| 45.7 |
|
| 0.51 |
|
| |||
| 5.1 | |||
表中![]() ,
,![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为声音强度
哪一个适宜作为声音强度![]() 关于声音能量的回归方程类型?(给出判断即可,不必说明理由)
关于声音能量的回归方程类型?(给出判断即可,不必说明理由)
(2)根据表中数据,求声音强度![]() 关于声音能量的回归方程;
关于声音能量的回归方程;
(3)当声音强度大于60分贝时属于噪音,会产生噪音污染,城市中某点![]() 共受到两个声源的影响,这两个声源的声音能量分别是
共受到两个声源的影响,这两个声源的声音能量分别是![]() 和
和![]() ,且
,且![]() .己知点
.己知点![]() 的声音能量等于声音能量
的声音能量等于声音能量![]() 与
与![]() 之和.请根据(1)中的回归方程,判断
之和.请根据(1)中的回归方程,判断![]() 点是否受到噪音污染的干扰,并说明理由.
点是否受到噪音污染的干扰,并说明理由.
附:对于一组数据![]() .其回归直线
.其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: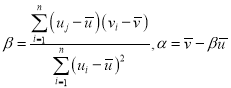 .
.