题目内容
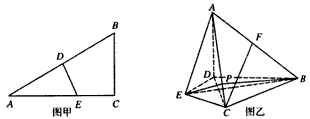
在△ABC中,∠ACB=90°,∠BAC=30°,AB的垂直平分线分别交AB,AC于D,E(图甲),沿DE将△ADE折起,使得平面ADE⊥平面BDEC(图乙)。
(Ⅰ)若F是AB的中点,求证:CF∥平面ADE;
(Ⅱ)P是AC上任意一点,求证:平面ACD⊥平面PBE;
(Ⅲ)P是AC上一点,且AC⊥平面PBE,求二面角P-BE-C的大小.
(Ⅰ)若F是AB的中点,求证:CF∥平面ADE;
(Ⅱ)P是AC上任意一点,求证:平面ACD⊥平面PBE;
(Ⅲ)P是AC上一点,且AC⊥平面PBE,求二面角P-BE-C的大小.
|
(Ⅰ)证明:取BD的中点为M,连接FM,CM, |
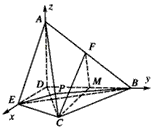 |

练习册系列答案
相关题目
 面CMF,
面CMF, ,则
,则 ,
, ,
, ,
, 如图,在△ABC中,AC=2,BC=1,
如图,在△ABC中,AC=2,BC=1, 如图,在△ABC中,AC=BC,AB=2,O为AB的中点,沿OC将△AOC折起到△A′OC的位置,使得直线A′B与平面ABC成30°角.
如图,在△ABC中,AC=BC,AB=2,O为AB的中点,沿OC将△AOC折起到△A′OC的位置,使得直线A′B与平面ABC成30°角.