题目内容
(08年扬州中学) 已知P是椭圆C:![]() 上异于长轴端点的任意一点,A为长轴的左端点,F为椭圆的右焦点,椭圆的右准线与x轴、直线AP分别交于点K、M,
上异于长轴端点的任意一点,A为长轴的左端点,F为椭圆的右焦点,椭圆的右准线与x轴、直线AP分别交于点K、M,![]() .
.
(Ⅰ)若椭圆的焦距为6,求椭圆C的方程;
(Ⅱ)若![]() ,求证:
,求证:![]() .
.

解析:(Ⅰ)解一:由![]() 得,
得,![]() ,
,![]() ,………………………2分
,………………………2分
∴ ![]() ,…………………………………………………………………4分
,…………………………………………………………………4分
从而椭圆方程是![]() .…………………………………………………………6分
.…………………………………………………………6分
解二:记![]() ,由
,由![]() ,
,
得 ,
,
∵![]() ,∴
,∴ ![]() ,………………………………………………………2分
,………………………………………………………2分
又![]() ,
,![]() ,∴
,∴ ![]() ,…………………………………………4分
,…………………………………………4分
从而椭圆方程是![]() . ………………………………………………………6分
. ………………………………………………………6分
(Ⅱ)解一:点![]() 同时满足
同时满足
![]() 和
和![]()
消去![]() 并整理得:
并整理得:![]() ,……………………………8分
,……………………………8分
此方程必有两实根,一根是点![]() 的模坐标
的模坐标![]() ,另一根是点
,另一根是点![]() 的模坐标
的模坐标![]() ,
,
![]() ,
,![]() ,…………………………………………10分
,…………………………………………10分
∴ ![]() ,
,
![]()
∴ ![]() ,…………………………12分
,…………………………12分
由![]() 代入上式可得
代入上式可得![]() .
.
∴ ![]() .
.![]() . ………………………………………………14分
. ………………………………………………14分
解二:由(Ⅰ)![]() ,
,![]() ,可设
,可设![]() ,
,![]() ,则
,则![]() ,
,
椭圆方程可为![]() ,即
,即![]() ,…………………………8分
,…………………………8分
设直线AM的方程为![]() (
(![]() 存在且
存在且![]() ),
),
代入![]() ,
,
整理得![]() ,…………………………10分
,…………………………10分
此方程两根为A、P两点的横坐标,
由韦达定理![]() ,
,![]()
∴ ![]() ,从而
,从而![]() .
.
由于![]()
![]() =
=![]()
![]() ,
,![]() , …………………………12分
, …………………………12分
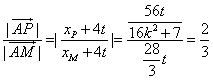
∴ ![]() .
.![]() . ………………………………………………14分
. ………………………………………………14分

练习册系列答案
相关题目