题目内容
【题目】某贫困地区几个丘陵的外围有两条相互垂直的直线型公路![]() ,
,![]() ,以及铁路线上的一条应开凿的直线穿山隧道
,以及铁路线上的一条应开凿的直线穿山隧道![]() ,为进一步改善山区的交通现状,计划修建一条连接两条公路
,为进一步改善山区的交通现状,计划修建一条连接两条公路![]() ,
,![]() 和山区边界的直线型公路
和山区边界的直线型公路![]() ,以
,以![]() ,
,![]() 所在的直线分别为
所在的直线分别为![]() 轴,
轴,![]() 轴,建立平面直角坐标系
轴,建立平面直角坐标系![]() ,如图所示,山区边界曲线为
,如图所示,山区边界曲线为![]() :
:![]() ,设公路
,设公路![]() 与曲线
与曲线![]() 相切于点
相切于点![]() .
.
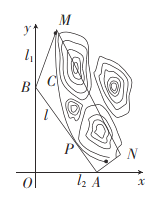
(1)设公路![]() 交
交![]() 轴,
轴,![]() 轴分别为
轴分别为![]() ,
,![]() 两点,若公路
两点,若公路![]() 的斜率为-1,求
的斜率为-1,求![]() 的长;
的长;
(2)在(1)条件下,测得四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 千米,
千米,![]() 千米,求应开凿的隧道
千米,求应开凿的隧道![]() 的长度.
的长度.
【答案】(1)![]() (千米);(2)
(千米);(2)![]() (千米)
(千米)
【解析】
(1)设点![]() 的坐标为
的坐标为![]() ,求得导数后由直线
,求得导数后由直线![]() 的斜率为
的斜率为![]() ,代入可求得切点的横坐标,代入即可求得切点坐标,进而表示出直线
,代入可求得切点的横坐标,代入即可求得切点坐标,进而表示出直线![]() 的方程,即可求得
的方程,即可求得![]() 的长;
的长;
(2)在![]() 中结合条件并由余弦定理可求得
中结合条件并由余弦定理可求得![]() ,同时由正弦定理可求得
,同时由正弦定理可求得![]() ,进而由
,进而由![]() 可求得
可求得![]() ,在
,在![]() 中由勾股定理可得
中由勾股定理可得![]() 的长.
的长.
(1)不妨设点![]() 的坐标为
的坐标为![]() ,曲线为
,曲线为![]() :
:![]() ,
,
则![]() ,
,
故![]() ,解得
,解得![]() ,
,
故![]() ,
,
所以直线方程为![]() ,
,
所以![]() (千米).
(千米).
(2)在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
所以由余弦定理可得![]() ,
,
代入可得![]() ,
,
根据正弦定理![]() ,
,
∴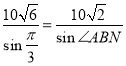 ,
,
∴![]() ,即
,即![]() ,
,
又![]() ,
,
所以![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
由勾股定理可得![]() ,
,
即![]() ,
,
解得![]() (千米).
(千米).

练习册系列答案
相关题目
【题目】袋子中有四张卡片,分别写有“学、习、强、国”四个字,有放回地从中任取一张卡片,将三次抽取后“学”“习”两个字都取到记为事件![]() ,用随机模拟的方法估计事件
,用随机模拟的方法估计事件![]() 发生的概率,利用电脑随机产生整数0,1,2,3四个随机数,分别代表“学、习、强、国”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
发生的概率,利用电脑随机产生整数0,1,2,3四个随机数,分别代表“学、习、强、国”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
232 | 321 | 210 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
由此可以估计事件![]() 发生的概率为( )
发生的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()