题目内容
 如图,已知△AOB,∠AOB=
如图,已知△AOB,∠AOB= ,∠BAO=
,∠BAO= ,AB=4,D为线段AB的中点.若△AOC是△AOB绕直线AO旋转而成的.记二面角B-AO-C的大小为θ.
,AB=4,D为线段AB的中点.若△AOC是△AOB绕直线AO旋转而成的.记二面角B-AO-C的大小为θ.
(1)当平面COD⊥平面AOB时,求θ的值;
(2)当θ∈[ ,
, ]时,求二面角C-OD-B的余弦值的取值范围.
]时,求二面角C-OD-B的余弦值的取值范围.
 解:(1)如图,以O为原点,在平面OBC内垂直于OB的直线为x轴,OB,OA所在的直线分别为y轴,z轴建立空间直角坐标系O-xyz,
解:(1)如图,以O为原点,在平面OBC内垂直于OB的直线为x轴,OB,OA所在的直线分别为y轴,z轴建立空间直角坐标系O-xyz,则O(0,0,0),A(0,0,2
 ),B(0,2,0),
),B(0,2,0),D (0,1,
 ),C (2sinθ,2cosθ,0).
),C (2sinθ,2cosθ,0). ,
, .
.设
 =(x,y,z)为平面COD的一个法向量,
=(x,y,z)为平面COD的一个法向量,由
 得
得
取z=sinθ,得:
 ,
, .
.则
 =(
=( cosθ,-
cosθ,- sinθ,sinθ).
sinθ,sinθ).因为平面AOB的一个法向量为
 =(1,0,0),
=(1,0,0),由平面COD⊥平面AOB得
 •
• =0,
=0,所以cosθ=0,即θ=
 .
. (2)设二面角C-OD-B的大小为α,
由(1)得,当θ=
 时,cosα=0;
时,cosα=0;当θ∈(
 ,
, ]时,tanθ≤-
]时,tanθ≤- ,
,cosα=
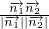 =
= =
= =-
=- ,
,∵tanθ≤-
 ,∴4tan2θ+3≥15,
,∴4tan2θ+3≥15,则
 .
.故-
 ≤cosα<0.
≤cosα<0.综上,二面角C-OD-B的余弦值的取值范围为[-
 ,0].
,0].分析:(1)以O点为坐标原点,OB,OA所在直线分别为y,z轴建立空间直角坐标系,把C点的坐标用含有θ的三角式表示,求出平面COD与平面AOB的法向量,由法向量的数量积等于0即可求得θ的值;
(2)由(1)得到当
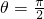 时的二面角C-OD-B的余弦值,当θ∈(
时的二面角C-OD-B的余弦值,当θ∈( ,
, ]时,把二面角的余弦值转化为它们的两个半平面的法向量所成角的余弦值,最后转化为角θ的正切值求解.
]时,把二面角的余弦值转化为它们的两个半平面的法向量所成角的余弦值,最后转化为角θ的正切值求解.点评:本题考查了面面垂直的判定,考查了二面角的平面角,解答此题的关键是明确二面角的平面角与它们的法向量所成角的关系,此题是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

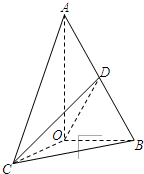 如图,已知△AOB,∠AOB=
如图,已知△AOB,∠AOB=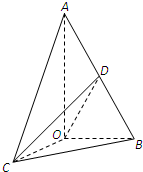 (2011•江西模拟)如图,已知△AOB,∠AOB=
(2011•江西模拟)如图,已知△AOB,∠AOB= 如图,已知△AOB,∠AOB=
如图,已知△AOB,∠AOB=