题目内容
已知椭圆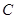 :
: =1(a>b>0)与双曲线
=1(a>b>0)与双曲线 有公共焦点,且离心率为
有公共焦点,且离心率为 .
.  分别是椭圆
分别是椭圆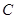 的左、右顶点. 点
的左、右顶点. 点 是椭圆
是椭圆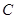 上位于
上位于 轴上方的动点.直线
轴上方的动点.直线 分别与直线
分别与直线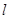 :
: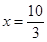 交于
交于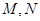 两点.
两点.
(I)求椭圆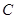 的方程;
的方程;
(II)当线段 的长度最小时,在椭圆
的长度最小时,在椭圆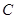 上是否存在点
上是否存在点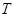 ,使得
,使得 的面积为
的面积为 ?若存在,求出
?若存在,求出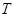 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.

【答案】
解:(I)由已知得椭圆 的焦点为
的焦点为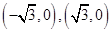 ,
,
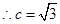 ,又
,又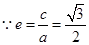 ,
,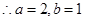 ,椭圆的方程为
,椭圆的方程为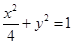 . ……..(4分)
. ……..(4分)
(II)直线 的斜率
的斜率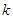 显然存在,且
显然存在,且 ,故可设直线
,故可设直线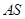 的方程为
的方程为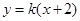 ,从而
,从而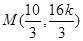 ……..(5分)
……..(5分)
由 得
得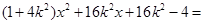 0
0
设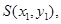 则
则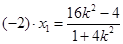 得
得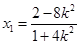 从而
从而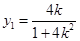
即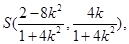 所以
所以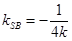
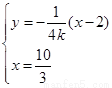 得
得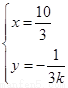
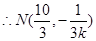 …….
……..(7分)
…….
……..(7分)
故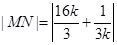 又
又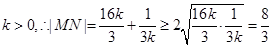
当且仅当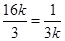 ,即
,即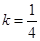 时等号成立
时等号成立
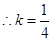 时,线段
时,线段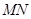 的长度取最小值
的长度取最小值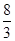 .
……..(9分)
.
……..(9分)
此时 的方程为
的方程为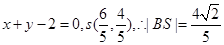
要使椭圆 上存在点
上存在点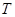 ,使得
,使得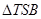 的面积等于
的面积等于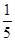 ,只须
,只须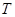 到直线
到直线 的距离等于
的距离等于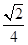 ,所以
,所以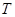 在平行于
在平行于 且与
且与 距离等于
距离等于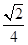 的直线
的直线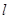 上.设直线
上.设直线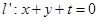
则由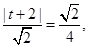 解得
解得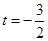 或
或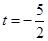
①当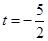 时由
时由 得
得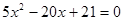 ,由于
,由于 故直线
故直线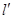 与椭圆没有交点.
与椭圆没有交点.
②当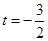 时,由
时,由 ,得
,得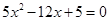
由于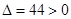 ,故直线
,故直线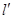 与椭圆
与椭圆 有两个不同的交点
有两个不同的交点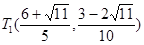 或
或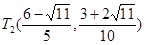 ;
;
综上所述,当线段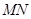 的长度最小时,在椭圆
的长度最小时,在椭圆 上仅存在两个不同的点
上仅存在两个不同的点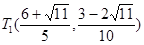 或
或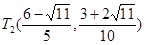 ,使得
,使得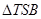 的面积为
的面积为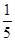 .
……………..(12分)
.
……………..(12分)
【解析】略

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 +
+ =1(a>b>0)与双曲线
=1(a>b>0)与双曲线 -
- =1有相同的焦点,则椭圆的离心率为
=1有相同的焦点,则椭圆的离心率为 B.
B. C.
C. D.
D.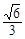
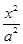 +
+ =1(a>b>0)上的点M(1,
=1(a>b>0)上的点M(1,
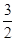 )到它的两焦点F1,F2的距离之和为4,A、B分别是它的左顶点和上顶点。
)到它的两焦点F1,F2的距离之和为4,A、B分别是它的左顶点和上顶点。