题目内容
如下图所示将若干个点摆成三角形图案,每条边(色括两个端点)有n(n>l,n∈N*)个点,相应的图案中总的点数记为an,则 +
+ +
+ +…+
+…+ =( )
=( )
A. | B. | C. | D. |
B
解析试题分析:由已知图形可知

 +
+ +
+ +…+
+…+


考点:数列求通项求和
点评:观察数列前4项得到通项,代入后采用裂项相消法求和,此法一般适用于通项公式为 形式的数列求和
形式的数列求和

练习册系列答案
相关题目
等差数列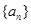 、
、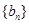 的前n项和分别为
的前n项和分别为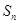 和
和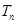 ,若
,若 ,则
,则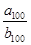 = ( )
= ( )
| A.1 | B.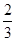 | C.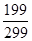 | D.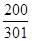 |
已知等差数列 的通项公式为
的通项公式为 ,设
,设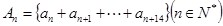 ,则当
,则当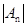 取得最小值是,n的值是 ( )
取得最小值是,n的值是 ( )
| A.17 | B.16 | C.15 | D.13 |
已知等差数列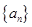 满足
满足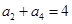 ,
, 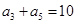 ,则它的前10项和
,则它的前10项和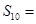 ( )
( )
| A.85 | B.135 | C.95 | D.23 |
数列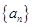 的通项公式
的通项公式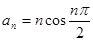 ,其前
,其前 项和为
项和为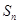 ,则
,则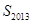 等于 ( )
等于 ( )
A.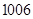 | B.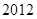 | C. | D. |
在一列数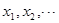 中,已知
中,已知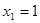 ,且当
,且当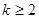 时,
时,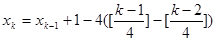 ,其中,
,其中,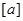 表示不超过实数
表示不超过实数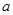 的最大整数(如
的最大整数(如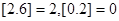 )则
)则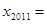 ( )
( )
A.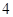 | B.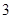 | C.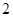 | D. |
已知数列 满足
满足 ,
, ,
, ,若数列
,若数列 满足
满足 ,则
,则 ( )
( )
A. | B. | C. | D. |
设数列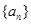 的前n项和为
的前n项和为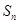 ,令
,令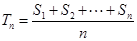 ,称
,称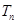 为数列
为数列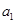 ,
,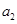 , ,
, ,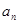 的“理想数”,已知数列
的“理想数”,已知数列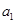 ,
,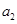 , ,
, ,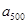 的“理想数”为2004,那么数列2,
的“理想数”为2004,那么数列2, 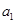 ,
,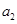 , ,
, ,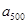 的“理想数”为
的“理想数”为
| A.2008 | B.2004 | C.2002 | D.2000 |
在数列 中,
中, 则
则 的值为 ( )
的值为 ( )
| A.49 | B. 50 | C.51 | D.52 |