Question

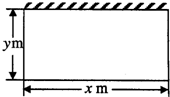某单位计划建一长方体状的仓库，底面如图，高度为定值．仓库的后墙和底部不花钱，正面的造价为40元/m，两侧的造价为45元/m，顶部的造价为20元/m²．设仓库正面的长为x（m），两侧的长各为y（m）．
（1）用x，y表示这个仓库的总造价t（元）；
（2）若仓库底面面积S=100m²时，仓库的总造价t最少是多少元，此时正面的长应设计为多少m？

Answer 1

分析：（1）仓库的总造价t=正面造价+两侧造价+顶部造价，代入即可；
（2）把仓库底面面积S=xy=100m² 代入函数t，利用基本不等式求其最小值以及x的值即可．

解答：解：（1）如图所示，
由题意，仓库的总造价为：t=40x+45×2y+20xy（元）；
（2）仓库底面面积S=xy=100m² 时，t=40x+45×2y+20xy=40x+90y+2000 ≥2

40x•90y

+2000=1200+2000=3200，当且仅当40x=90y 时，等号成立，
又∵xy=100，∴x=15（m）．
所以，当仓库底面面积S=100m² 时，仓库的总造价最少是3200 元，此时正面的长应设计为15m．

点评：本题考查了利用基本不等式a+b≥2

ab

（其中a＞0，b＞0）求函数最值的问题，属于基础题目．