题目内容
已知函数 .
.
(1)求f(x)的单调区间;
(2)求曲线y=f(x)在点x=1处的切线方程;
(3)求曲线y=f(x),y=|x|所围成的图形的面积S.
解:(1)∵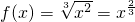 ,∴
,∴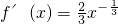
解f'(x)>0得x>0,解f'(x)<0得x<0,
∴f(x)的单调增区间是(0,+∞),单调减区间是(-∞,0)
(注:也可以写成闭区间[0,+∞)或(-∞,0])…(4分)
(2)切点坐标是(1,1),且 ,
,
∴y=f(x)在点x=1处的切线方程是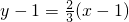
化简得2x-3y+1=0…(9分)
(3)解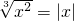 得x=±1,0
得x=±1,0
由 的图象特点得曲线y=f(x),y=|x|所围成的图形的面积是:
的图象特点得曲线y=f(x),y=|x|所围成的图形的面积是:
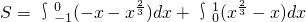 =
=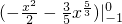 +
+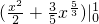 =
=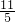 .(14分)
.(14分)
分析:(1)求导函数,由导数的正负可得函数的单调区间;
(2)确定确定坐标与切线的斜率,可得切线方程;
(3)确定积分区间与被积函数,即可求得曲线y=f(x),y=|x|所围成的图形的面积S.
点评:本题考查导数知识的运用,考查函数的单调性,考查切线方程,考查利用定积分求面积,综合性强,属于中档题.
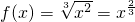 ,∴
,∴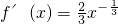
解f'(x)>0得x>0,解f'(x)<0得x<0,
∴f(x)的单调增区间是(0,+∞),单调减区间是(-∞,0)
(注:也可以写成闭区间[0,+∞)或(-∞,0])…(4分)
(2)切点坐标是(1,1),且
 ,
,∴y=f(x)在点x=1处的切线方程是
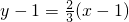
化简得2x-3y+1=0…(9分)
(3)解
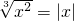 得x=±1,0
得x=±1,0由
 的图象特点得曲线y=f(x),y=|x|所围成的图形的面积是:
的图象特点得曲线y=f(x),y=|x|所围成的图形的面积是: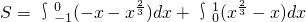 =
=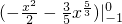 +
+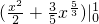 =
=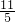 .(14分)
.(14分)分析:(1)求导函数,由导数的正负可得函数的单调区间;
(2)确定确定坐标与切线的斜率,可得切线方程;
(3)确定积分区间与被积函数,即可求得曲线y=f(x),y=|x|所围成的图形的面积S.
点评:本题考查导数知识的运用,考查函数的单调性,考查切线方程,考查利用定积分求面积,综合性强,属于中档题.

练习册系列答案
相关题目
 .
. .
. 的图象在x轴上方?
的图象在x轴上方? .
. 为f(x)的一个零点,求sin2x的值.
为f(x)的一个零点,求sin2x的值.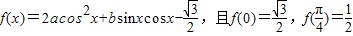 .
. .
. ,求f(x)的最大值和最小值.
,求f(x)的最大值和最小值.